北京市东城区2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2018-01-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、x+x²=x³ B、x²·x³ =x⁶ C、（x³）² =x⁶ D、x⁹÷x³=x³

查看试题解析
3. 下列式子为最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{4}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
4. 如果 $\sqrt{x - 2}$ 有意义，那么x的取值范围是（）

A、x>2 B、x≥2 C、x≤2 D、x<2

查看试题解析
5. 如图，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于点D，如果AC=3cm，那么AE+DE等于（）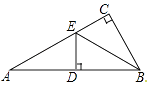

A、2cm B、3cm C、4cm D、5cm

查看试题解析
6. 如图，所示的图形面积由以下哪个公式表示（）

A、a² -b² =a（a-b）+b（a-b） B、（a-b）² =a² -2ab+b² C、（a+b）² =a² +2ab+b² D、a²-b²=（a-b）（a+b）

查看试题解析
7. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为（）

A、x=1 B、x=-1 C、x=±1 D、x≠1

查看试题解析
8. 若x- $\frac{1}{x}$ =1，则x²+ $\frac{1}{x^{2}}$ 的值是（）

A、3 B、2 C、1 D、4

查看试题解析
9. 如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC，AD，AB于点E，O，F，连接OC，OB，则图中全等的三角形有（）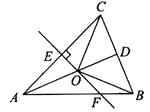

A、1对 B、2对 C、3对 D、4对

查看试题解析
10. 如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（）

A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、2 $\sqrt{6}$ D、 $\sqrt{6}$

查看试题解析

二、填空题

11. 中国女药学家屠呦呦获2015年诺贝尔医学奖，她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素，这是中国医学界迄今为止获得的最高奖项．已知显微镜下的某种疟原虫平均长度为0.0000015米，该长度用科学记数法表示为．

查看试题解析
12. 如图，AB=AC，点E，点D分别在AC，AB上，要使△ABE≌△ACD，应添加的条件是.（添加一个条件即可）

查看试题解析
13. 若x² +2（m-3）x+16是一个完全平方式，那么m应为.

查看试题解析
14. 如图，Rt△ABC的斜边AB的中垂线MN与AC交于点M，∠A=15°，BM=2，则△AMB的面积为.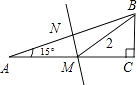

查看试题解析
15. 在平面直角坐标系xOy中，已知点A（2，3），在坐标轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有个．

查看试题解析

三、解答题

16. 观察下列关于自然数的等式：
3² -4×1² =5 ①
5² -4×2² =9 ②
7² -4×3² =13 ③
根据上述规律解决下列问题：

(1)、完成第四个等式：；

(2)、写出你猜想的第n个等式（用含n的式子表示）.

查看试题解析
17. 因式分解：

(1)、4x² -9

(2)、3ax² -6axy+3ay²

查看试题解析
18. 计算：

(1)、[（2x+3y）² -（2x+y）（2x-y）] ÷2y

(2)、（2 $\sqrt{12}$ -6 $\sqrt{\frac{1}{3}}$ +3 $\sqrt{48}$ ）÷2 $\sqrt{3}$

查看试题解析
19. 先化简，再求值： $\frac{x + 2}{2 x^{2} - 4 x}$ ÷（x-2+ $\frac{8 x}{x - 2}$ ），其中x= $\sqrt{2}$ -1.

查看试题解析
20. 解方程： $\frac{x}{x - 2}$ - $\frac{1}{x^{2} - 4}$ =1.

查看试题解析
21. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A（2，3），B（3，1），C（-2，-2）.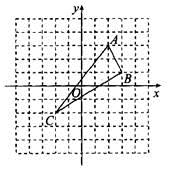

(1)、请在图中作出△ABC关于y轴的轴对称图形△A′B′C′（A，B，C的对称点分别是A′，B′，C′），并直接写出A′，B′，C′的坐标.

(2)、求△A′B′C′的面积.

查看试题解析
22. 如图，点C，D在线段BF上，AB∥DE，AB=DF，∠A=∠F.
求证：△ABC≌△FDE.

查看试题解析
23. 如图，在△ABC中，BD平分∠ABC，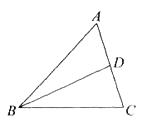

(1)、作图：作BC边的垂直平分线分别交BC，BD于点E，F（用尺规作图法，保留作图痕迹，不要求写作法）；

(2)、在（1）的条件下，连接CF，若∠A=60°，∠ABD=24°，求∠ACF的度数.

查看试题解析
24. 在△ABC中，∠A=60°，∠ABC，∠ACB所对的边b，c满足：b $^{2}$ +c $^{2}$ -4（b+c）+8=0.

(1)、证明：△ABC是边长为2的等边三角形.

(2)、若 b，c两边上的中线BD，CE交于点O，求OD：OB的值.

查看试题解析
25. 2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年.某商家用1200元购进了一批抗战主题纪念衫，上市后果然供不应求，商家又用2800元购进了第二批这种纪念衫，所购数量是第一批购进量的2倍，但单价贵了5元.

(1)、该商家购进的第一批纪念衫是多少件？

(2)、若两批纪念衫按相同的标价销售，最后剩下20件按八折优惠卖出，如果两批纪念衫全部售完利润率不低于16％（不考虑其它因素），那么每件纪念衫的标价至少是多少元？

查看试题解析
26. 如图①，在△ABC中，D、E分别是AB，AC上的点，AB=AC，AD=AE，然后将△ADE绕点A顺时针旋转一定角度，连接BD，CE，得到图②，将BD，CE分别延长至M，N，使DM= $\frac{1}{2}$ BD，EN= $\frac{1}{2}$ CE，连接AM，AN，MN得到图③，请解答下列问题：

(1)、在图②中，BD与CE的数量关系是；

(2)、在图③中，猜想AM与AN的数量关系，∠MAN与∠BAC的数量关系，并证明你的猜想.

查看试题解析