2017-2018学年北师大版八年级上学期数学期末模拟试卷

试卷更新日期：2018-01-10 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数0，π， $\frac{22}{7}$ ， $\sqrt{2}$ ， $- \sqrt{9}$ 中，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 估计 $\sqrt{32} \times \sqrt{\frac{1}{2}} + \sqrt{20}$ 的运算结果应在（）

A、6到7之间 B、7到8之间 C、8到9之间 D、9到10之间

查看试题解析
3. 下列计算错误的是（）

A、3＋2 $\sqrt{2}$ ＝5 $\sqrt{2}$ B、 $\sqrt{8}$ ÷2＝ $\sqrt{2}$ C、 $\sqrt{2}$ × $\sqrt{3}$ ＝ $\sqrt{6}$ D、 $\sqrt{8}$ － $\sqrt{2}$ ＝ $\sqrt{2}$

查看试题解析
4. 如图，若象棋盘上建立直角坐标系，使“将”位于点(1，－2)，“象”位于点(3，－2)，则“炮”位于点（）

A、(1，－1) B、(－1，1) C、(－1，2) D：(1，－2)

查看试题解析
5. 我国古代数学名著《孙子算经》记载一道题，大意为：100个和尚吃了100个馒头，已知1个大和尚吃3个馒头，3个小和尚吃1个馒头，问有几个大和尚，几个小和尚？若设有m个大和尚，n个小和尚，那么可列方程组为（）

A、 ${\begin{array}{l} m + n = 100 \\ 3 m + 3 n = 100 \end{array}$ B、 ${\begin{array}{l} m + n = 100 \\ m + 3 n = 100 \end{array}$ C、 ${\begin{array}{l} m + n = 100 \\ 3 m + n = 100 \end{array}$ D、 ${\begin{array}{l} m + n = 100 \\ m + \frac{n}{3} = 100 \end{array}$

查看试题解析
6.
为迎接2013年“亚青会”，学校组织了一次游戏：每位选手朝特制的靶子上各投三次飞镖，在同一圆环内得分相同．如图所示，小明、小君、小红的成绩分别是29分、43分和33分，则小华的成绩是（　　）

A、31分 B、33分 C、36分 D、38分

查看试题解析
7. 如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于x、y的二元一次方程组的解是（）

A、 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ B、 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = - 3 \\ y = 1 \end{matrix}$ D、 ${\begin{matrix} x = 3 \\ y = 1 \end{matrix}$

查看试题解析
8. 为确保信息安全，信息需加密传输，发送方将明文加密文件传输给接收方，接收方收到密文后解密还原为明文，已知某种加密规则为，明文a、b对应的密文为a+2b，2a﹣b，例如：明文1，2对应的密文是5，0，当接收方收到的密文是1，7时，解密得到的明文是（　　）

A、3，﹣1 B、1，﹣3 C、﹣3，1 D、﹣1，3

查看试题解析
9. 已知一组数据为：10，8，10，12，10．其中中位数、平均数和众数的大小关系是（）

A、众数=中位数=平均数 B、中位数＜众数＜平均数 C、平均数＞中位数＞众数 D、平均数＜中位数＜众数

查看试题解析
10. 如图，AD平分∠BAC，DE∥AC交AB于点E，∠1=25°，则∠BED等于（）

A、40° B、50° C、60° D、25°

查看试题解析
11. 把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为（）

A、125° B、120° C、140° D、130°

查看试题解析
12.
如图，一架云梯25米，斜靠在一面墙上，梯子底端离墙7米，如果梯子的顶端下滑4米，那么梯子的底部在水平方向上滑动了（　　）

A、4米 B、6米 C、8米 D、10米

查看试题解析

二、填空题

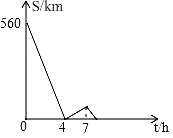
13. 将直线y=2x向下平移2个单位，所得函数的图象过第象限．

查看试题解析
14. 一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后分别按原速同时驶往甲地，两车之间的距离S（km）与慢车行驶时间t（h）之间的函数图象如图所示，则快车到达甲地时，慢车距离甲地 km．

查看试题解析
15. 七年级（2）班有46人报名参加文学社或书画社．已知参加文学社的人数比参加书画社的人数多10人，两社都参加的有20人，则参加书画社的有人．

查看试题解析
16. 如图是某市2013﹣2016年私人汽车拥有量和年增长率的统计量，该市私人汽车拥有量年净增量最多的是年，私人汽车拥有量年增长率最大的是年．

查看试题解析
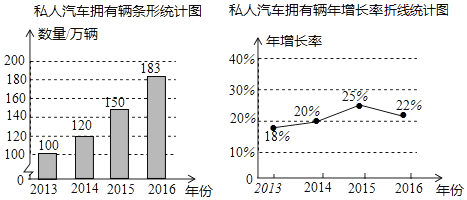17. 一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是．

查看试题解析
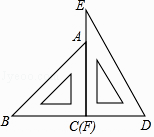18. 如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF=°．

查看试题解析
19. 要使代数式 $\frac{\sqrt{x + 1}}{x}$ 有意义，则x的取值范围是．

查看试题解析
20.
如图，在△ABC中，∠C=90°，∠C=90°，AB=5，BC=4，AC=3，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，则△BDE的周长为．

查看试题解析

三、计算题

21. 计算：（π﹣2016）⁰+（ $\frac{1}{3}$ ）^﹣1﹣ $\sqrt{4}$ ×|﹣3|．

查看试题解析
22. 计算： $\sqrt{48}$ + $\sqrt{3}$ （ $\sqrt{3}$ ﹣1）﹣3⁰﹣| $\sqrt{3}$ ﹣2|．

查看试题解析

四、解答题

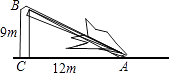
23. 如图，一根树在离地面9米处撕裂，树的顶部落在离底部12米处，求折断之前树高多少米．

查看试题解析
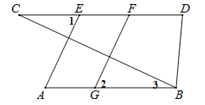
24.
已知：如图，AE⊥BC，FG⊥BC，∠1=∠2，∠D=∠3+60°，∠CBD=70°．
（1）求证：AB∥CD；
（2）求∠C的度数．

查看试题解析
25.
如图在△ABC中，AD⊥BC，垂足为D，E是AC边上一点，BE与AD交于点F，若∠ABC=45°，∠BAC=75°，∠BFD=60°．求∠BEC的度数．

查看试题解析

五、综合题

26. 甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y（件）．甲车间加工的时间为x（时），y与x之间的函数图象如图所示．

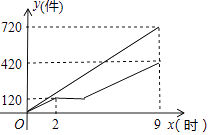(1)、甲车间每小时加工服装件数为件；这批服装的总件数为件．

(2)、求乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式；

(3)、求甲、乙两车间共同加工完1000件服装时甲车间所用的时间．

查看试题解析
27. 某中学了解本校学生对球类运动的爱好情况，分为足球、篮球、排球、其他四个方面调查若干名学生，每人只选其中之一，统计后绘制成不完整的“折线统计图”（扇形统计图），根据信息解答下列问题：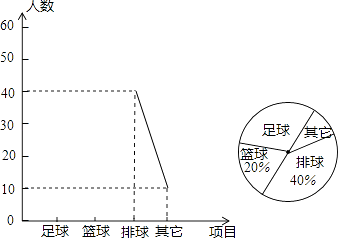

(1)、在这次调查中，一共调查名学生；

(2)、在扇形统计图中，“足球”所在扇形圆心角度；

(3)、将折线统计图补充完整．

查看试题解析