2017-2018学年人教版八年级上学期数学期末模拟试卷
试卷更新日期:2018-01-10 类型:期末考试
一、单选题
-
1. 下列四组线段中(单位cm),能组成三角形的是( )A、2,3,4 B、3,4,7 C、4,6,2 D、7,10,22. 无论x取何值时,下列分式中总有意义的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、全等三角形是指形状相同的两个三角形 B、全等三角形的周长和面积分别相等 C、全等三角形是指面积相等的两个三角形 D、所有的等边三角形都是全等三角形4. 在分式 (a,b为正数)中,字母a,b值分别扩大为原来的2倍,则分式的值( )A、扩大为原来的2倍 B、缩小为原来的 C、不变 D、不确定5. 如图是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若固定其形状,下列有四种加固木条的方法,不能固定形状的是钉在( )两点上的木条.
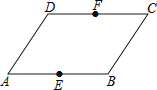 A、A和F B、C和E C、C和A D、E和F6. 等腰三角形的一个角是48°,它的一个底角的度数是( )A、48° B、48°或42° C、42°或66° D、48°或66°7. 若关于x的分式方程 + =2有增根,则m的值是( )A、m=﹣1 B、m=0 C、m=3 D、m=0或m=38.
A、A和F B、C和E C、C和A D、E和F6. 等腰三角形的一个角是48°,它的一个底角的度数是( )A、48° B、48°或42° C、42°或66° D、48°或66°7. 若关于x的分式方程 + =2有增根,则m的值是( )A、m=﹣1 B、m=0 C、m=3 D、m=0或m=38.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
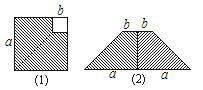 A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣b2=(a﹣b)29. 今年我市工业试验区投资50760万元开发了多个项目,今后还将投资106960万元开发多个新项目,每个新项目平均投资比今年每个项目平均投资多500万元,并且新增项目数量比今年多20个.假设今年每个项目平均投资是x万元,那么下列方程符合题意的是( )A、 ﹣ =20 B、 ﹣ =20 C、 ﹣ =500 D、 ﹣ =50010.
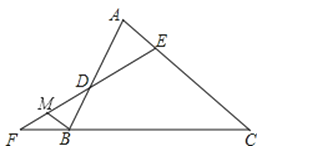
A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣b2=(a﹣b)29. 今年我市工业试验区投资50760万元开发了多个项目,今后还将投资106960万元开发多个新项目,每个新项目平均投资比今年每个项目平均投资多500万元,并且新增项目数量比今年多20个.假设今年每个项目平均投资是x万元,那么下列方程符合题意的是( )A、 ﹣ =20 B、 ﹣ =20 C、 ﹣ =500 D、 ﹣ =50010.如图,△ABC的顶点分别为A(0,3),B(﹣4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
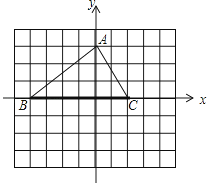 A、(﹣2,﹣3) B、(2,﹣3) C、(2,3) D、(0,3)11.
A、(﹣2,﹣3) B、(2,﹣3) C、(2,3) D、(0,3)11.若关于x的分式方程
 =2的解为非负数,则m的取值范围是( ).A、m>﹣1 B、m≥1 C、m>﹣1且m≠1 D、m≥﹣1且m≠112.
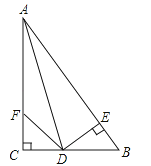
=2的解为非负数,则m的取值范围是( ).A、m>﹣1 B、m≥1 C、m>﹣1且m≠1 D、m≥﹣1且m≠112.如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
①∠CFE=∠CEF;②∠FCB=∠FBC,③∠A=∠DCB;④∠CFE与∠CBF互余.
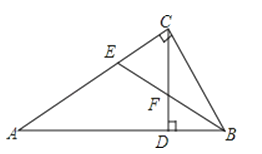 A、①③④ B、②③④ C、①②④ D、①②③
A、①③④ B、②③④ C、①②④ D、①②③二、填空题
-
13. 计算:(-3)2= .
14. 分解因式:2x2﹣8xy+8y2= .15. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于 .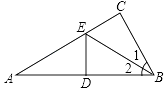 16.
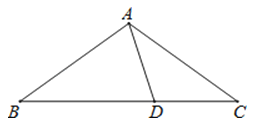
16.如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为 .
 17. 如图,在△ABC中∠ABC和∠ACB平分线交于点O,过点O作OD⊥BC于点D,△ABC的周长为18,OD=4,则△ABC的面积是 .
17. 如图,在△ABC中∠ABC和∠ACB平分线交于点O,过点O作OD⊥BC于点D,△ABC的周长为18,OD=4,则△ABC的面积是 .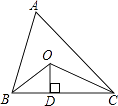 18. 我们把不相等的两个实数a,b中较大实数a记作max{a,b}=a,例如:max{2.3,3.4}=3.4,
18. 我们把不相等的两个实数a,b中较大实数a记作max{a,b}=a,例如:max{2.3,3.4}=3.4,max{﹣5.6,﹣8.7}=﹣5.6,max{﹣3,0}=0…那么:关于x的方程 的解是 .
三、作图题
-
19. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
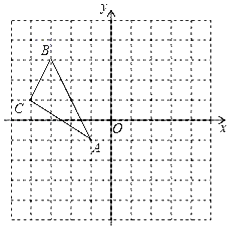
①画出△ABC关于y轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;
②画出△ABC向下平移3个单位的△A2B2C2 , 并写出点C的对应点C2的坐标.
四、解答题
-
20. 先化简,再求值:5(3a2b﹣ab2)﹣3(ab2+5a2b),其中a= , b=﹣ .21. 先化简,再求值: ,其中 .22.
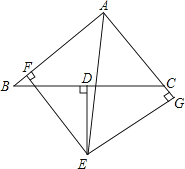
如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,
EF⊥AB于F,EG⊥AG交AC的延长线于G.求证:BF=CG.
 23.
23.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
 24. 几个小伙伴打算去音乐厅观看演出,他们准备用360元钱购买门票.下面是两个小伙伴的对话:
24. 几个小伙伴打算去音乐厅观看演出,他们准备用360元钱购买门票.下面是两个小伙伴的对话:
根据对话的内容,请你求出小伙伴们的人数.
-