2017-2018学年人教版九年级上学期数学期末模拟试卷
试卷更新日期:2018-01-09 类型:期末考试
一、单选题
-
1. 如果点A(x1 , y1)和点B(x2 , y2)是直线y=kx﹣b上的两点,且当x1<x2时,y1<y2 , 那么函数y=的图象位于( )象限.A、一、四 B、二、四 C、三、四 D、一、三2. 如图,在同一平面直角坐标系中,直线y=k1x(k1≠0)与双曲线y= (k2≠0)相交于A,B两点,已知点A的坐标为(1,2),则点B的坐标为( )
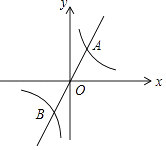 A、(﹣1,﹣2) B、(﹣2,﹣1) C、(﹣1,﹣1) D、(﹣2,﹣2)3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
A、(﹣1,﹣2) B、(﹣2,﹣1) C、(﹣1,﹣1) D、(﹣2,﹣2)3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、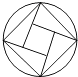 C、
C、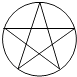 D、
D、 4. 如图,在⊙O中,AB=BC,点D在⊙O上,∠CDB=25°,则∠AOB=( )
4. 如图,在⊙O中,AB=BC,点D在⊙O上,∠CDB=25°,则∠AOB=( )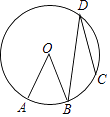 A、45° B、50° C、55° D、60°5. 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A、45° B、50° C、55° D、60°5. 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( ) A、2米 B、2.5米 C、2.4米 D、2.1米6.
A、2米 B、2.5米 C、2.4米 D、2.1米6.如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
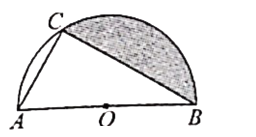 A、 B、 C、 D、7. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )A、
A、 B、 C、 D、7. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )A、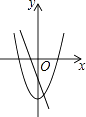 B、
B、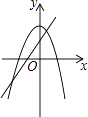 C、
C、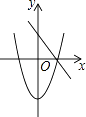 D、
D、 8.
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
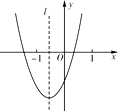 A、a<0 B、c>0 C、a+b+c>0 D、b2-4ac<09. 下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
A、a<0 B、c>0 C、a+b+c>0 D、b2-4ac<09. 下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:x
1
1.1
1.2
1.3
1.4
y
﹣1
﹣0.49
0.04
0.59
1.16
那么方程x2+3x﹣5=0的一个近似根是( )
A、1 B、1.1 C、1.2 D、1.310. 已知一元二次方程2x2﹣5x+1=0的两个根为x1 , x2 , 下列结论正确的是( )A、x1+x2=﹣ B、x1•x2=1 C、x1 , x2都是有理数 D、x1 , x2都是正数11. 已知a﹣b=1,则a2﹣b2﹣2b的值为( )A、1 B、2 C、3 D、412. 关于x的一元二次方程x2﹣2x+k=0有两个相等的实数根,则k的值为( )A、1 B、﹣1 C、2 D、﹣2二、填空题
-
13. 已知x=1是方程ax2+x﹣6=0的一个根,则a= .14. 小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2﹣2b+3,若将实数对(x,﹣3x)放入其中,得到一个新数为5,则x= .15. 若(a2+b2﹣1)2=16,则a2+b2值为 .16. 已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
3
﹣2
﹣5
﹣6
﹣5
…
则关于x的一元二次方程ax2+bx+c=﹣2的根是 .
17. 已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论:①b<1;②c<2;③0<m< ;④n≤1.
则所有正确结论的序号是 .
18. 用12m长的木材做窗框(如图所示),要使透过窗户的光线最多,窗框的长应为 m,宽应为 m. 19. 如图,点E,F在函数y= 的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:3,则△EOF的面积是 .
19. 如图,点E,F在函数y= 的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:3,则△EOF的面积是 .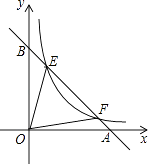 20. 如图,△AOB与反比例函数 交于C、D,且AB∥x轴,△AOB的面积为6,若AC:CB=1:3,则反比例函数的表达式为 .
20. 如图,△AOB与反比例函数 交于C、D,且AB∥x轴,△AOB的面积为6,若AC:CB=1:3,则反比例函数的表达式为 .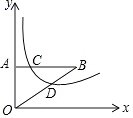
三、解答题
-
21. 交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)、根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ② ③(2)、请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?(3)、已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:①市交通运行监控平台显示,当 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值
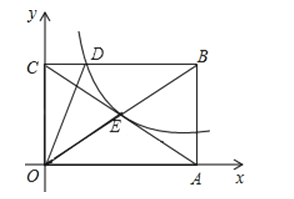
22. 如图,反比例函数y=在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).(1)求E点的坐标及k的值;
(2)求△OCD的面积.
 23. 某地大力发展经济作物,其中果树种植已初具规模,今年受气候、雨水等因素的影响,樱桃较去年有小幅度的减产,而枇杷有所增产.(1)、该地某果农今年收获樱桃和枇杷共400千克,其中枇杷的产量不超过樱桃产量的7倍,求该果农今年收获樱桃至少多少千克?(2)、该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售,该果农去年樱桃的市场销售量为100千克,销售均价为30元/千克,今年樱桃的市场销售量比去年减少了m%,销售均价与去年相同,该果农去年枇杷的市场销售量为200千克,销售均价为20元/千克,今年枇杷的市场销售量比去年增加了2m%,但销售均价比去年减少了m%,该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额比他去年樱桃和枇杷的市场销售总金额相同,求m的值.24. 如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
23. 某地大力发展经济作物,其中果树种植已初具规模,今年受气候、雨水等因素的影响,樱桃较去年有小幅度的减产,而枇杷有所增产.(1)、该地某果农今年收获樱桃和枇杷共400千克,其中枇杷的产量不超过樱桃产量的7倍,求该果农今年收获樱桃至少多少千克?(2)、该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售,该果农去年樱桃的市场销售量为100千克,销售均价为30元/千克,今年樱桃的市场销售量比去年减少了m%,销售均价与去年相同,该果农去年枇杷的市场销售量为200千克,销售均价为20元/千克,今年枇杷的市场销售量比去年增加了2m%,但销售均价比去年减少了m%,该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额比他去年樱桃和枇杷的市场销售总金额相同,求m的值.24. 如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.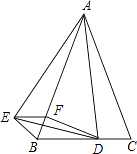 (1)、求证:BE=CD;(2)、若AD⊥BC,试判断四边形BDFE的形状,并给出证明.25. 如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)、求证:BE=CD;(2)、若AD⊥BC,试判断四边形BDFE的形状,并给出证明.25. 如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.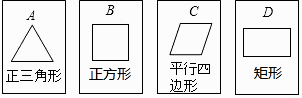 (1)、从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;(2)、小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).26. 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
(1)、从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;(2)、小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).26. 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.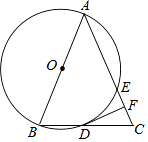 (1)、求证:DF是⊙O的切线;(2)、若AE=4,cosA= ,求DF的长.
(1)、求证:DF是⊙O的切线;(2)、若AE=4,cosA= ,求DF的长.