辽宁省葫芦岛市2016-2017学年高二下学期文数期末考试试卷

试卷更新日期：2018-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 ${(a - i)}^{2} = - 2 i$ ，其中 $i$ 是虚数单位，则实数 $a$ =（）

A、-2 B、-1 C、1 D、2

查看试题解析
2. 用列举法可以将集合 $A = {a | a$ 使方程 $a x^{2} + 2 x + 1 = 0$ 有唯一实数解 $}$ 表示为（）

A、 $A = {1}$ B、 $A = {0}$ C、 $A = {0, 1}$ D、 $A = {0}$ 或 ${1}$

查看试题解析
3. 甲、乙、丙、丁四位歌手参加比赛，只有其中一位获奖．有人走访了四位歌手，甲说：“是乙或丙获奖．”乙说：“甲、丙都未获奖．”丙说：“我获奖了．”丁说：“是乙获奖．”四位歌手的话只有两句是对的，则获奖的歌手是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 下列函数中，值域为 $[0, 1]$ 的是（）

A、 $y = x^{2}$ B、 $y = sin x$ C、 $y = \frac{1}{x^{2} + 1}$ D、 $y = \sqrt{1 - x^{2}}$

查看试题解析
5. 函数 $f (x) = x^{3} + a x^{2} + 3 x - 9$ ，已知 $f (x)$ 在 $x = - 3$ 时取得极值，则 $a$ = （）

A、2 B、3 C、4 D、5

查看试题解析
6. 设函数f（x）（x∈R）为奇函数，f（1）= $\frac{1}{2}$ ，f（x+2）=f（x）+f（2），则f（5）=（）

A、0 B、1 C、 $\frac{5}{2}$ D、5

查看试题解析
7. 用反证法证明命题：“若整系数一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有有理数根，那么 $a$ 、 $b$ 、 $c$ 中至少有一个是偶数”时，下列假设中正确的是（）

A、假设 $a$ 、 $b$ 、 $c$ 都是偶数 B、假设 $a$ 、 $b$ 、 $c$ 都不是偶数 C、假设 $a$ 、 $b$ 、 $c$ 中至多有一个是偶数 D、加速 $a$ 、 $b$ 、 $c$ 中至多有两个是偶数

查看试题解析
8. 执行下面的程序框图，如果输入 $a = 4$ ，那么输出的 $n$ 的值为（）

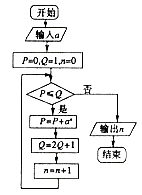A、2 B、3 C、4 D、5

查看试题解析
9. 下列结论中正确的是（）

A、若两个变量的线性关系性越强，则相关系数的绝对值越接近于0 B、回归直线至少经过样本数据中的一个点 C、独立性检验得到的结论一定正确 D、利用随机变量 $x^{2}$ 来判断“两个独立事件 $X, Y$ 的关系”时，算出的 $x^{2}$ 值越大，判断“ $X, Y$ 有关”的把握越大

查看试题解析
10. 从某高中随机选取5名高三男生，其身高和体重的数据如下表所示：
身高 $x (c m)$
160
165
170
175
180
体重 $y (k g)$
63
66
70
72
74
根据上表可得到回归直线方程 $\hat{y} = 0.65 x + \hat{a}$ ，据此模型预报身高为172 $c m$ 的高三男生的体重为（）

A、70.09 $k g$ B、70.12 $k g$ C、70.55 $k g$ D、71.05 $k g$

查看试题解析
11. 定义在 $(0 ， + \infty)$ 上的单调递减函数 $f (x)$ ，若 $f (x)$ 的导函数存在且满足 $\frac{f (x)}{f' (x)} > x$ ，则下列不等式成立的是（）

A、 $3 f (2) < 2 f (3)$ B、 $3 f (4) < 4 f (3)$ C、 $2 f (3) < 3 f (4)$ D、 $f (2) < 2 f (1)$

查看试题解析
12. 已知函数 $f (x) = {\begin{matrix} \frac{2^{x} + 2}{2} (x \leq 1) \\ | {log}_{2} (x - 1) | (x > 1) \end{matrix}$ ，则函数 $F (x) = f [f (x)] - 2 f (x) - \frac{3}{2}$ 的零点个数是（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

13. 函数 $f (x) = lg x + \sqrt{2 - x}$ 的定义域为.

查看试题解析
14. 观察下列各式：a+b=1，a²+b²=3，a³+b³=4，a⁴+b⁴=7，a⁵+b⁵=11，…，则a¹⁰+b¹⁰=

查看试题解析
15. 设函数 $f (x) = {\begin{matrix} 2^{1 - x} (x \leq 1) \\ 1 - {log}_{2} x (x > 1) \end{matrix}$ ，则满足 $f (x) \leq 2$ 的 $x$ 的取值范围是.

查看试题解析
16. 设点 $P$ 在曲线 $y = x^{2} + 1 (x \geq 0)$ 上，点 $Q$ 在曲线 $y = \sqrt{x - 1} (x \geq 1)$ 上，则 $| P Q |$ 的最小值为.

查看试题解析

三、解答题

17. 已知集合 $A = {x | x^{2} - 3 x + 2 = 0}$ ， $B = {x | x^{2} - a x + a - 1 = 0}$ ，若 $A \cup^{} B = A$ ，求 $a$ 的值.

查看试题解析
18. 已知函数 $f (x) = a x^{2} + b x + 1$ （ $a$ ， $b$ 为实数， $a \neq 0$ ， $x \in R$ ）

(1)、若函数 $f (x)$ 的图象过点 $(- 2 ， 1)$ ，且方程 $f (x) = 0$ 有且只有一个实根，求 $f (x)$ 的表达式；

(2)、在（1）的条件下，当 $x \in [- 1 ， 2]$ 时， $g (x) = f (x) - k x$ 是单调函数，求实数 $k$ 的取值范围.

查看试题解析
19. 已知函数 $f (x) = x^{3} + a x^{2} + b x + 5$ .

(1)、若曲线 $f (x)$ 在点 $(1 ， f (1))$ 处的切线斜率为3，且 $x = \frac{2}{3}$ 时 $y = f (x)$ 有极值，求函数 $f (x)$ 的解析式；

(2)、在（1）的条件下，求函数 $f (x)$ 在 $[- 4 ， 1]$ 上的最大值和最小值.

查看试题解析
20. 某厂商为了解用户对其产品是否满意，在使用产品的用户中随机调查了80人，结果如下表：

(1)、根据上述，现用分层抽样的方法抽取对产品满意的用户5人，在这5人中任选2人，求被选中的恰好是男、女用户各1人的概率；

(2)、有多大把握认为用户对该产品是否满意与用户性别有关？请说明理由.
$P (K^{2} \geq k)$
0.15
0.10
0.05
0.025
0.010
0.005
0.001
$k$
2.072
2.706
3.841
5.024
6.635
7.879
10.828
注： $k^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$

查看试题解析
21. 已知函数 $f (x) = e^{x} - x^{2} - 1$ ， $x \in R$

(1)、求函数的图象在点 $(0 ， f (0))$ 处的切线方程；

(2)、当 $x \in R$ 时，求证： $f (x) \geq x^{2} + x$ ；

(3)、若 $f (x) > k x$ 对任意的 $x \in (0 ， + \infty)$ 恒成立，求实数 $k$ 的取值范围.

查看试题解析
22. 在直角坐标系 $x O y$ 中，曲线 $C$ 的方程为 ${(x - 1)}^{2} + {(y - 1)}^{2} = 2$ ，直线 $l$ 的倾斜角为 $45 °$ 且经过点 $P (- 1 ， 0)$ .

(1)、以 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系，求曲线 $C$ 的极坐标方程；

(2)、设直线 $l$ 与曲线 $C$ 交于两点 $A$ ， $B$ ，求 $\frac{1}{| P A |} + \frac{1}{| P B |}$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x - 1 | + | x + a |$ .

(1)、当 $a = 2$ 时，解不等式 $f (x) \geq 4$ ；

(2)、若 $a > 0$ ，求 $\forall x \in R$ ， $f (x) \geq 5$ 恒成立，求 $a$ 的取值范围.

查看试题解析

$P (K^{2} \geq k)$	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$k$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

身高 $x (c m)$	160	165	170	175	180
体重 $y (k g)$	63	66	70	72	74