浙江省宁波市鄞州区2017-2018学年九年级上学期数学第一次月考试卷
试卷更新日期：2018-01-08 类型：月考试卷
一、单选题
-
1. 下列事件是必然事件的是（ ）
A、三点确定一个圆 B、三角形内角和180度 C、明天是晴天 D、打开电视正在放广告2. 将抛物线 的图象先向上平移3个单位，再向右平移4个单位所得的解析式为（ ）A、 B、 C、 D、3. 已知一个布袋里装有2个红球，3个白球和a个黄球，这些球除颜色外其余都相同．若从该布袋里任意摸出1个球，是红球的概率为 ，则a等于（ ）A、1 B、2 C、3 D、44. 下列命题中，不正确的是（ ）A、垂直平分弦的直线经过圆心 B、平分弦的直径一定垂直于弦 C、平行弦所夹的两条弧相等 D、垂直于弦的直径必平分弦所对的弧5. 已知（﹣1，y1），（﹣2，y2），（﹣4，y3）是抛物线y=﹣2x2﹣8x+m上的点，则（ ）A、y1＜y2＜y3 B、y3＜y2＜y1 C、y3＜y1＜y2 D、y2＜y3＜y16. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=20°，则∠B的度数是（ ）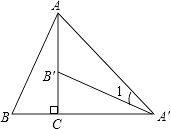
A、70° B、65° C、60° D、55°7. 如图，圆心在y轴的负半轴上，半径为5的⊙B与y轴的正半轴交于点A（0，1），过点P（0，﹣7）的直线l与⊙B相交于C，D两点．则弦CD长的所有可能的整数值有（ ）
A、1个 B、2个 C、3个 D、4个8. 一次函数 和 同一直角坐标系内的图象是（ ）A、
B、
C、
D、
9. 下列每张方格纸上都有一个三角形，只用圆规就能做出三角形的外接圆的是（ ）
① 
② 
③ 
④A、①② B、①③ C、②④ D、③④10. 二次函数y＝a(x－4)2－4(a≠0)的图象在2＜x＜3这一段位于x轴的下方，在6＜x＜7这一段位于x轴的上方，则a的值为（ ）
A、1 B、－1 C、2 D、－211. 如图，等腰Rt△ABC（∠ACB=90°）的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让△ABC沿这条直线向右平移，直到点A与点E重合为止．设CD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）
A、
B、
C、
D、
12. 如图，已知抛物线y=ax2+bx+c（a＜0）的对称轴为x=1，交x轴的一个交点为（x1 ， 0），且﹣1＜x1＜0，有下列5个结论：①abc＞0；②9a﹣3b+c＜0；③2c＜3b；④（a+c）2＜b2；⑤a+b＞m（am+b）（m≠1的实数）其中正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 一圆的半径是10cm，圆内的两条平行弦长分别为12cm和16cm，则这两条平行弦之间的距离为 ．
14. 甲、乙、丙三人站成一排合影留念，则甲、乙二人相邻的概率是 ．15. 抛物线y=kx2﹣7x﹣7的图象和x轴有交点，则k的取值范围是 ．
16.如图，在平面直角坐标系中，抛物线y=x2经过平移得到抛物线y=x2﹣2x，其对称轴与两抛物线所围成的阴影部分的面积是 ．
17. 如图，平行于x轴的直线AC分别交抛物线 （x≥0）与 （x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则 = ．
18. 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=(x-1)2-4，AB为半圆的直径，求这个“果圆”被y轴截得的弦CD的长 ．
三、解答题
-
19. 如图，有一转盘中有A、B两个区域，A区域所对的圆心角为120°，让转盘自由转动两次．利用树状图或列表求出两次指针都落在A区域的概率。
20. 已知抛物线经过点（4，3），且当 时， 有最小值 .
(1)、求这条抛物线的解析式.
(2)、写出 随 的增大而减小的自变量 的取值范围.
21. 已知二次函数y=x2﹣4x+3．
(1)、求函数图象的对称轴、顶点坐标、与坐标轴交点的坐标，并画出函数的大致图象；
(2)、根据图象直接写出函数值y为负数时，自变量x的取值范围．
22. 如图，抛物线y=ax2+bx+c与x轴相交于两点A（1，0），B（3，0），与y轴相交于点C（0，3）．
(1)、求抛物线的函数关系式.(2)、将y=ax2+bx+c化成y=a（x﹣m）2+k的形式(请直接写出答案).
(3)、若点D（3.5，m）是抛物线y=ax2+bx+c上的一点，请求出m的值，并求出此时△ABD的面积．
23. 某工厂准备翻建新的大门，厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m，最大高度OC=4m，工厂的运输卡车的高度是3m，宽度是5.8m.现设计了两种方案.方案一：建成抛物线形状（如图1）；方案二：建成圆弧形状（如图2）.为确保工厂的卡车在通过厂门时更安全，你认为应采用哪种设计方案？请说明理由.
24. 某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．
(1)、不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
(2)、在（1）条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元．
(3)、在（1）条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
25. 如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．
(1)、求抛物线的解析式；(2)、若直线BC的函数解析式为y’=kx+b，求当满足y<y’时，自变量x的取值范围.
(3)、平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标．