浙江省宁波市鄞州区2017-2018学年八年级上学期数学第一次月考试卷
试卷更新日期：2018-01-08 类型：月考试卷
一、单选题
-
1. 下列长度的三条线段不可能组成三角形的是（ ）A、1、2、3 B、2、3、4 C、3、4、5 D、4、5、62. 如图，已知∠ABC＝∠BAD ， 添加下列条件还不能判定△ABC≌△BAD的是（ ）
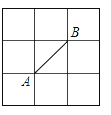
A、AC＝BD B、∠CAB＝∠DBA C、∠C＝∠D D、BC＝AD3.如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（ ）
A、6 B、7 C、8 D、94. 能够将一个三角形的面积平分的线段是（ ）A、一边上的高线 B、一个内角的角平分线 C、一边上的中线 D、一边上的中垂线5. 能说明命题“对于任意实数a，a＞-a”是假命题的一个反例是（ ）A、a= B、a=1.5 C、a=4 D、a=-226. 如图，已知每个小方格的边长为1，A、B、C三点都在小方格的顶点上，则点C到AB所在直线的距离等于（ ）
A、 B、 C、 D、7. 已知等腰三角形一腰上的中线将它的周长分成9cm和12cm两部分，则等腰三角形的底边长为（ ）A、9cm B、5cm C、6cm或5cm D、5cm或9cm8. 如图，在下列三角形中，若AB=AC，则能被一条直线分成两个小等腰三角形的是（ ）
A、(1)(2)(3) B、(1)(2)(4) C、(2)(3)(4) D、(1)(3)(4)9. 如图所示，在△ABC中，已知点D、E、F分别是BC、AD、CE的中点，且 ＝4，则 的值是（ ）
A、1 B、1.5 C、2 D、2.510. 如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连结BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④∠ACE=∠DBC其中结论正确的个数有（ ）
A、4 B、3 C、2 D、1二、填空题
-
11. 观察下列图形： 其中是轴对称图形的有个.
12. 如图，B，C，D在同一直线上，∠B＝∠D＝90°，AB＝CD，BC＝DE，则△ACE的形状为.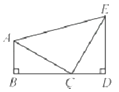
13. 如图，在△ABC中，AC=10cm，DE是AB的中垂线，△BDC的周长为16cm，则BC的长为 ．
14. 命题“等腰三角形的两个底角相等．”的逆命题是 ．15. 若直角三角形的两条边长为a、b，且满足 ，则该直角三角形的斜边长为16. 在△ABC中，与∠A相邻的外角是140°要使△ABC是等腰三角形，则∠B 的度数是.
17. 如图在△ABC中，BF、CF是角平分线，DE∥BC，分别交AB、AC于点D、E，DE经过点F．结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE； ③△ADE的周长=AB+AC；④BF=CF．其中正确的是（填序号）
18. 如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为 .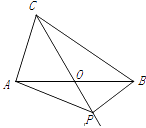
三、解答题
-
19. 已知：如图，在△ABC中，∠A=30°，∠B=60°．
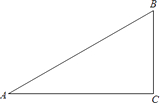(1)、①作∠B的平分线BD，交AC于点D；②作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作法和证明）；
(2)、连接DE，求证：△ADE≌△BDE．20. 如图，在△ABC中，∠B=∠C，D为BC的中点， E为AC的中点，AB=6，求DE的长。
21. 如图，在△ABC 中，∠B=32°，∠C =48°，AD⊥BC于点D，AE平分∠BAC交BC于点E，DF⊥AE于点F，求∠ADF的度数.
