浙江省宁波市鄞州区2016-2017学年八年级下学期数学期中考试试卷

试卷更新日期：2018-01-08 类型：期中考试

进入出卷网下载

一、单选题

1. 下面这几个车标中，是中心对称图形而不是轴对称图形的共有（）

A、1 B、2 C、3 D、4

查看试题解析
2. 若反比例函数y＝ $\frac{k}{x}$ 的图象经过点(2，－1)，则该反比例函数的图象在（）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
3. 下列各数中，可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是（）

A、5 B、4 C、8 D、6

查看试题解析
4. 下列条件不能用来判定四边形ABCD是平行四边形的是（）

A、∠A：∠B：∠C：∠D=1：4：1：4 B、AB∥CD，AD=BC C、AB=CD，AD=BC D、AB∥CD，AD∥CB

查看试题解析
5. 如图．在菱形ABCD中，对角线AC，BD交于点O，下列说法错误的是（）

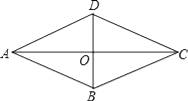A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OC

查看试题解析
6. 若P（m，a），Q（ $\frac{1}{m}$ ，b）两点均在函数y=﹣ $\frac{2}{x}$ 的图象上，且﹣1＜m＜0，则a﹣b的值为（）

A、正数 B、负数 C、零 D、非负数

查看试题解析
7.
如图，▱ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取值范围是（）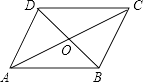

A、1＜m＜11 B、2＜m＜22 C、10＜m＜12 D、5＜m＜6

查看试题解析
8. 如图，平面直角坐标系中，平行四边形OABC的顶点C（3，4），边OA落在x正半轴上，P为线段AC上一点，过点P分别作DE∥OC，FG∥OA交平行四边形各边如图．若反比例函数 $y = \frac{k}{x}$ 的图象经过点D，四边形BCFG的面积为8，则k的值为（）

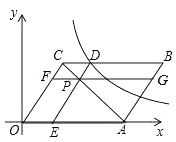A、16 B、20 C、24 D、28

查看试题解析

二、填空题

9. 如果反比例函数y= $\frac{k - 1}{x}$ 的图象经过点（﹣1，﹣2），则k的值是．

查看试题解析
10. 如图，将平行四边形ABCD的一边BC延长至E，若∠A=110°，则∠1= ．

查看试题解析
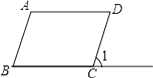11. 若矩形ABCD的两邻边长分别为一元二次方程x²﹣7x+12=0的两个实数根，则矩形ABCD的对角线长为．

查看试题解析
12. 菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF= $\sqrt{2}$ ，BD=2，则菱形ABCD的面积为．

查看试题解析
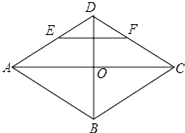13. 以正方形ABCD两条对角线的交点O为坐标原点，建立如图所示的平面直角坐标系，双曲线y= $\frac{3}{x}$ 经过点D，则正方形ABCD的面积是．

查看试题解析
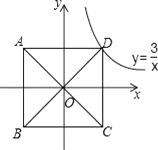14. 如图，在▱ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为．

查看试题解析
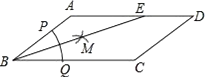15.
如图，已知矩形ABCD的对角线长为8cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长等于cm．

查看试题解析
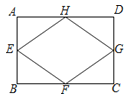16. 如图，已知点A在反比例函数 $y = \frac{4}{x}$ 的图象上，点B在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，AB∥x轴，分别过点A、B作x轴作垂线，垂足分别为C、D，若OC= $\frac{1}{3}$ OD ，则k的值为．

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=6cm，点P从点A出发，沿AB方向以每秒 $\sqrt{2}$ cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′，设Q点运动的时间为t秒，若四边形QPCP′为菱形，则t的值为．

查看试题解析
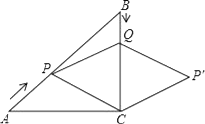18. 如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，BE与CD相交于点G，且OE=OD，则AP的长为．

查看试题解析

三、解答题

19. 如图，已知正比例函数y=3x的图象与反比例函数y= $\frac{k}{x}$ 的图象交于点A（1，m）和点B．

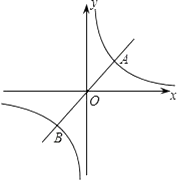(1)、求m的值和反比例函数的解析式．

(2)、观察图象，直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围．

查看试题解析
20. 如图，在平行四边形ABCD中，E、F分别在AD、BC边上，且AE=CF．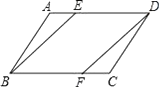
求证：

(1)、△ABE≌△CDF；

(2)、四边形BFDE是平行四边形．

查看试题解析
21. 如图，在平面直角坐标系中，矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB，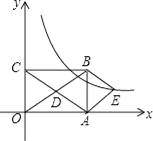

(1)、求证：四边形AEBD是菱形；

(2)、如果OA=3，OC=2，求出经过点E的反比例函数解析式．

查看试题解析
22. 如图，点O是线段AB上的一点，OA=OC，OD平分∠AOC交AC于点D，OF平分∠COB，CF⊥OF于点F．

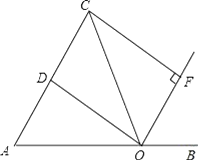(1)、求证：四边形CDOF是矩形；

(2)、当∠AOC多少度时，四边形CDOF是正方形？并说明理由．

查看试题解析
23. 如图1，有一张菱形纸片ABCD，AC=8，BD=6．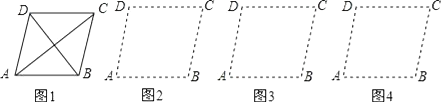

(1)、请沿着AC剪一刀，把它分成两部分，把剪开的两部分拼成一个平行四边形，在图2中用实线画出你所拼成的平行四边形；若沿着BD剪开，请在图3中用实线画出拼成的平行四边形；并直接写出这两个平行四边形的周长．

(2)、沿着一条直线剪开，拼成与上述两种都不全等的平行四边形，请在图4中用实线画出拼成的平行四边形．（注：上述所画的平行四边形都不能与原菱形全等）

查看试题解析
24. 定义：有一个内角为90°，且对角线相等的四边形称为准矩形．

(1)、①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=；
②如图2，直角坐标系中，A（0，3），B（5，0），若整点P使得四边形AOBP是准矩形，则点P的坐标是；（整点指横坐标、纵坐标都为整数的点）

(2)、如图2，正方形ABCD中，点E、F分别是边AD、AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；

(3)、已知，准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是．

查看试题解析