浙江省宁波市宁海县东片2015届九年级上学期数学第三次月考试卷
试卷更新日期:2018-01-08 类型:月考试卷
一、单选题
-
1. 二次函数 的图象的对称轴是( )A、直线x= -3 B、直线 x=3 C、直线x= -1 D、直线x=12. 若 ,则 ( )A、 B、 C、 D、-3. 将抛物线y=3x2的图象先向上平移3个单位,再向右平移4个单位所得的解析式为( )
A、y=3(x-3)2+4 B、y=3(x+4)2-3 C、y=3(x-4)2+3 D、y=3(x-4)2-34. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,那么sinA的值等于( )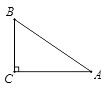 A、 B、 C、 D、5. 下列语句中不正确的有 ( )
A、 B、 C、 D、5. 下列语句中不正确的有 ( )①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④半圆是弧.
A、1个 B、2个 C、3个 D、4个6. 在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色,…如此大量摸球实验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,对此实验,他总结出下列结论:①若进行大量摸球实验,摸出白球的频率稳定于30%,②若从布袋中任意摸出一个球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是( )A、①②③ B、①② C、①③ D、②③7. 如图,点A,B,C在⊙O上,已知∠ABC=130°,则∠AOC=( )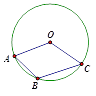 A、100° B、110° C、120° D、130°8. 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AE∶AC = 3∶4,AD=6,则BD等于( )
A、100° B、110° C、120° D、130°8. 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AE∶AC = 3∶4,AD=6,则BD等于( )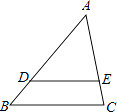 A、8 B、6 C、4 D、29. 在⊙O 中,P是⊙O内一点,过点P最短和最长的弦分别为6和10,则经过点P且长度为整数的的弦共有( )条。A、5 B、8 C、10 D、无数条10. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )
A、8 B、6 C、4 D、29. 在⊙O 中,P是⊙O内一点,过点P最短和最长的弦分别为6和10,则经过点P且长度为整数的的弦共有( )条。A、5 B、8 C、10 D、无数条10. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( ) A、
A、 B、
B、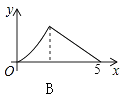 C、
C、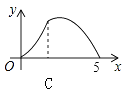 D、
D、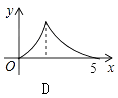 11. 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , ………按这样的规律进行下去,第2012个正方形的面积为( )
11. 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , ………按这样的规律进行下去,第2012个正方形的面积为( )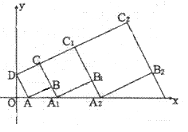 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 数3和12的比例中项是 。
13. 直角三角形的两直角边长分别为8和6,则此三角形的外接圆半径是__14. 如图,有五张背面完全相同的纸质卡片,其正面分别标有数:6、 、 、-2、 .将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数比3小的概率是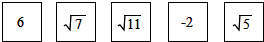 15. 如图,矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 .
15. 如图,矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 .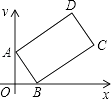 16. 如图,AB是⊙O的直径,弦BC=4㎝,F是弦BC的中点,∠ABC=60°,若动点E以1 ㎝/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t(s)的值为
16. 如图,AB是⊙O的直径,弦BC=4㎝,F是弦BC的中点,∠ABC=60°,若动点E以1 ㎝/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t(s)的值为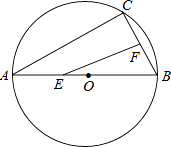 17. 半圆O的直径AB=9,两弦AC、BD相交于点E,弦CD= ,且BD=7,则DE=
17. 半圆O的直径AB=9,两弦AC、BD相交于点E,弦CD= ,且BD=7,则DE=
三、解答题
-
18. 计算题
(1)、已知:sinα·cos60º= ,求锐角α;
(2)、计算: .19. 如图,圆心角∠AOB=120°,弦AB=2 cm.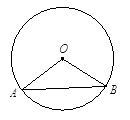 (1)、求⊙O的半径r;
(1)、求⊙O的半径r;
(2)、求劣弧 的长(结果保留 ).
20. 网格中每个小正方形的边长都是1.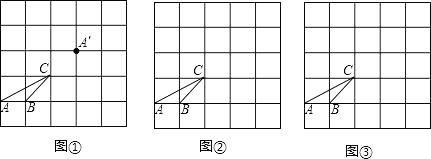 (1)、将图①中的格点三角形ABC平移,使点A平移至点A`,画出平移后的三角形;(2)、在图②中画一个格点三角形DEF,使△DEF∽△ABC,且相似比为2∶1;(3)、在图③中画一个格点三角形PQR,使△PQR∽△ABC,且相似比为 ∶1.21. 将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面
(1)、将图①中的格点三角形ABC平移,使点A平移至点A`,画出平移后的三角形;(2)、在图②中画一个格点三角形DEF,使△DEF∽△ABC,且相似比为2∶1;(3)、在图③中画一个格点三角形PQR,使△PQR∽△ABC,且相似比为 ∶1.21. 将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面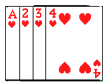 (1)、从中随机抽出一张牌,试求出牌面数字是偶数的概率;
(1)、从中随机抽出一张牌,试求出牌面数字是偶数的概率;
(2)、先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
22. 如图, △ABC内接于⊙O, AD⊥BC于D, AE是⊙O的直径. 若AB=6, AC=8, AE=11, 求AD的长.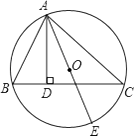 23. 我镇绿色和特色农产品在市场上颇具竞争力.外贸商胡经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如图)帮胡经理解决以下问题:
23. 我镇绿色和特色农产品在市场上颇具竞争力.外贸商胡经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如图)帮胡经理解决以下问题: (1)、若胡经理想将这批蘑菇存放x天后一次性出售, 则x天后这批蘑菇的销售单价为元, 这批蘑菇的销售量是千克;(2)、胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量).
(1)、若胡经理想将这批蘑菇存放x天后一次性出售, 则x天后这批蘑菇的销售单价为元, 这批蘑菇的销售量是千克;(2)、胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量).
(3)、将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?24. 对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(2,0)和抛物线E上的点B(-1,n),请完成下列任务:
 (1)、【尝试】
(1)、【尝试】①当t=2时,抛物线E的顶点坐标是.
②点A抛物线E上;(填“在”或“不在”),
③n=.
(2)、【发现】通过②和③的演算可知,对于t取任何不为零的实数,抛物线E总过定点,这个定点的坐标是.(3)、【应用1】二次函数y=-3x2+5x+2是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.(4)、【应用2】以AB为一边作矩形ABCD,使得其中一个顶点落在y轴上,若抛物线E经过点A、B、C,求出所有符合条件的t的值.
25. 如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).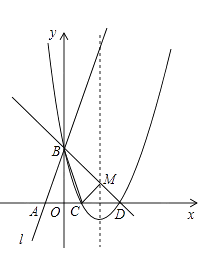 (1)、求直线BD和抛物线的解析式.(2)、若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(1)、求直线BD和抛物线的解析式.(2)、若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)、在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.