浙江省宁波市江东区2015届数学4月中考模拟试卷
试卷更新日期:2018-01-08 类型:中考模拟
一、单选题
-
1. 实数5的相反数是( )A、 B、 C、-5 D、52. 下列各式计算正确的是( )
A、a2•a3=a6 B、(﹣a3)2=a6 C、(2ab)4=8a4b4 D、2a2﹣3a2=13. 下列四个数中,值最小的数是( ).
A、tan45° B、 C、π D、4. 某热播视频10天的点击量达51234.8万次,把它用科学记数法表示是( ).A、5.12348×104次 B、0.512348×105次 C、5.12348×108次 D、5.12348×109次5. 如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( ).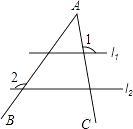 A、25° B、30° C、35° D、45°6. 要说明“若两个单项式的次数相同,则它们是同类项”是假命题,可以举的反例是( )A、2ab和3ab B、2a2b和3ab2 C、2ab和2a2b2 D、2a3和﹣2a37. 某药品经过两次降价,每瓶零售价由180元降为100元.已知两次降价的百分率相同,设每次降价的进分率为x,根据题意列方程正确的是( )A、180(1+x)2=100 B、180(1﹣x2)=100 C、180(1﹣2x)=100 D、180(1﹣x)2=1008. 若4个数6,x,8,10的中位数为7,则x的取值范围是( ).
A、25° B、30° C、35° D、45°6. 要说明“若两个单项式的次数相同,则它们是同类项”是假命题,可以举的反例是( )A、2ab和3ab B、2a2b和3ab2 C、2ab和2a2b2 D、2a3和﹣2a37. 某药品经过两次降价,每瓶零售价由180元降为100元.已知两次降价的百分率相同,设每次降价的进分率为x,根据题意列方程正确的是( )A、180(1+x)2=100 B、180(1﹣x2)=100 C、180(1﹣2x)=100 D、180(1﹣x)2=1008. 若4个数6,x,8,10的中位数为7,则x的取值范围是( ).
A、x=6 B、x=7 C、x≤6 D、x≥89. 如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( )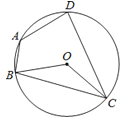 A、120° B、130° C、140° D、150°10. 如图,3个全等的菱形按如图方式拼合在一起,恰好得到一个边长相等的六边形,则菱形较长的对角线与较短的对角线之比是( )
A、120° B、130° C、140° D、150°10. 如图,3个全等的菱形按如图方式拼合在一起,恰好得到一个边长相等的六边形,则菱形较长的对角线与较短的对角线之比是( )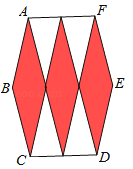 A、 B、 C、 D、11. 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿 回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( ).
A、 B、 C、 D、11. 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿 回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( ). A、
A、 B、
B、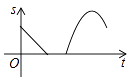 C、
C、 D、
D、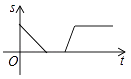 12. 下表中所列x,y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7 , 根据表中所提供的信息,以下判断正确的是( ).
12. 下表中所列x,y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7 , 根据表中所提供的信息,以下判断正确的是( ).①a>0;
②9<m<16;
③k≤9;
④b2≤4a(c﹣k).
x
…
x1
x2
x3
x4
x5
x6
x7
…
y
…
16
m
9
k
9
m
16
…
A、①② B、③④ C、①②④ D、①③④二、解答题
-
13. 解方程:+=5.14. 如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.
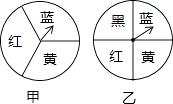 (1)、请你画树状图或列表表示所有等可能的结果.(2)、求两个指针落在区域的颜色能配成绿色的概率.(黄、蓝两色混合配成绿色)15. 如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.
(1)、请你画树状图或列表表示所有等可能的结果.(2)、求两个指针落在区域的颜色能配成绿色的概率.(黄、蓝两色混合配成绿色)15. 如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°. (1)、求梯子顶端A离地面的高度AD的长和两梯脚之间的距离BC的长.(2)、生活经验告诉我们,增大两梯脚之间的距离可降低梯子的高度,若BC长达到6米,则梯子的高度下降多少米?(以上结果均精确到0.1米,供参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)16. 如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)、求梯子顶端A离地面的高度AD的长和两梯脚之间的距离BC的长.(2)、生活经验告诉我们,增大两梯脚之间的距离可降低梯子的高度,若BC长达到6米,则梯子的高度下降多少米?(以上结果均精确到0.1米,供参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)16. 如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.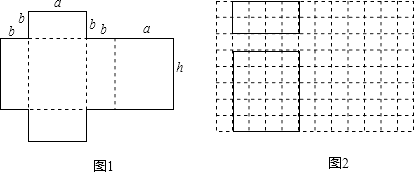 (1)、这个几何体模型的名称是(2)、如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(1)、这个几何体模型的名称是(2)、如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)、若h=a+b,且a,b满足 a2+b2﹣a﹣6b+10=0,求该几何体的表面积.17. 已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.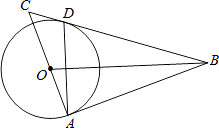 (1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为8,tan∠C= ,求线段AB的长,sin∠ADB的值.
(1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为8,tan∠C= ,求线段AB的长,sin∠ADB的值.
18. 某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).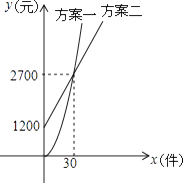 (1)、分别求两种方案中y关于x的函数关系式;(2)、当销售达到多少件时,两种方案月报酬差额将达到3800元?
(1)、分别求两种方案中y关于x的函数关系式;(2)、当销售达到多少件时,两种方案月报酬差额将达到3800元?
(3)、若公司决定改进“方案二”:保持基本工资不变,每件报酬增加m元,使得当销售员销售产量达到40件时,两种方案的报酬差额不超过1000元.求m的取值范围.
19. 【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变. (1)、【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
(1)、【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.求证:①ME=NF;②MN∥BC.
(2)、【解决问题】如图1,若BP=3,求线段MN的长;(3)、如图2,当点P与点Q重合时,求MN的长.20. 已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=﹣m(m> )于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.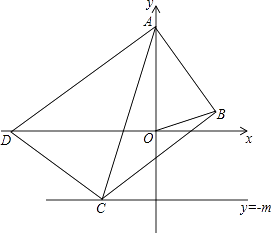 (1)、求证:△ABC≌△AOD;(2)、设△ACD的面积为S,求S关于m的函数关系式;
(1)、求证:△ABC≌△AOD;(2)、设△ACD的面积为S,求S关于m的函数关系式;
(3)、若四边形ABCD恰有一组对边平行,求m的值.三、填空题
-
21. 计算: = .22. 分解因式:a3﹣9a= .
23. 现有一圆心角为120°,半径为9cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则围成的圆锥的高为cm.
24. 某校为预测该校九年级900名学生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分学生进行测试,并以测试数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值).若次数不低于130次的成绩为优秀,估计该校成绩为优秀的人数是 .

