浙江省宁波市东钱湖九校2017-2018学年八年级上学期数学期中联考试卷
试卷更新日期:2018-01-08 类型:期中考试
一、单选题
-
1. 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )A、1,2,1 B、1,2,3 C、1,2,2 D、1,2,42. 若a>b,则下列各式中一定成立的是( )A、ma>mb B、a2>b2 C、1-a>1-b D、b-a<03. 如图,笑脸盖住的点的坐标可能为( )
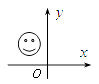 A、(5,2) B、(-2,3) C、(-4,-6) D、(3,-4)4. 已知一个等腰三角形一底角的度数为80°.则这个等腰三角形顶角的度数为( )A、20° B、70° C、80° D、100°5. 对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )A、∠1=50°,∠2=40° B、∠1=50°,∠2=50° C、∠1=∠2=45° D、∠1=40°,∠2=40°6. 已知点A(﹣3,2)与点B(x,y)在同一条平行x轴的直线上,且B点到y轴的距离等于2,则B点的坐标是( )A、(﹣2,2) B、(2,﹣2) C、(﹣2,2)或(﹣2,﹣2) D、(﹣2,2)或(2, 2)7. 小明到离家900米的春晖超市卖水果,从家中到超市走了20分钟,在超市购物用了10分钟,然后用15分钟返回家中,下列图形中表示小明离家的时间与距离之间的关系是( )A、
A、(5,2) B、(-2,3) C、(-4,-6) D、(3,-4)4. 已知一个等腰三角形一底角的度数为80°.则这个等腰三角形顶角的度数为( )A、20° B、70° C、80° D、100°5. 对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )A、∠1=50°,∠2=40° B、∠1=50°,∠2=50° C、∠1=∠2=45° D、∠1=40°,∠2=40°6. 已知点A(﹣3,2)与点B(x,y)在同一条平行x轴的直线上,且B点到y轴的距离等于2,则B点的坐标是( )A、(﹣2,2) B、(2,﹣2) C、(﹣2,2)或(﹣2,﹣2) D、(﹣2,2)或(2, 2)7. 小明到离家900米的春晖超市卖水果,从家中到超市走了20分钟,在超市购物用了10分钟,然后用15分钟返回家中,下列图形中表示小明离家的时间与距离之间的关系是( )A、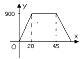 B、
B、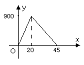 C、
C、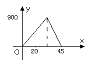 D、
D、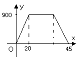 8. 下列的真命题中,它的逆命题也是真命题的有 ( )
8. 下列的真命题中,它的逆命题也是真命题的有 ( )①两直线平行,同旁内角互补;②等边三角形是锐角三角形;③两个图形关于某直线成轴对称,则这两个图形是全等图形;④若a=b,则a2=b2;⑤等腰三角形两底角相等.
A、①② B、①⑤ C、③④ D、④⑤9. 关于x的不等式组 有四个整数解,则a的取值范围是( )A、 B、 C、 D、10. 如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4 ,OC=10,O′为△ABC外一点,且△CBO≌△ABO′,则四边形AO′BO的面积为( )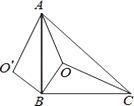 A、10 B、16 C、40 D、80
A、10 B、16 C、40 D、80二、填空题
-
11. 已知等腰三角形的其中两边长分别为4,9,则这个等腰三角形的周长为 .12. 若点M(1-m,2+m)在第四象限内,则m的取值范围是 .13. 如图,在△ABC中,DE是AC的垂直平分线,AE=4,△ABD的周长为14,则△ABC的周长为 .
 .14. 将点P(-2,y)先向下平移4个单位,再向左平移2个单位后得到点Q(x,-1),则x+y= .
.14. 将点P(-2,y)先向下平移4个单位,再向左平移2个单位后得到点Q(x,-1),则x+y= .
15. 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB的中点,分别以ED,EC为折痕将两个角,(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=4,BC=9,则EF的值是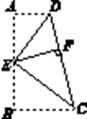 16. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2 , AB=16cm,AC=14cm,则DE= .
16. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2 , AB=16cm,AC=14cm,则DE= .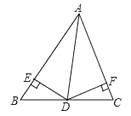 17. 勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 .
17. 勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 .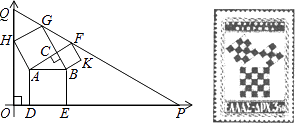
三、解答题
-
18. 解不等式组 ,把解表示在数轴上,并写出该不等式组的非负整数解.19. 如图,△ABC中,AB=BC , ∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF .
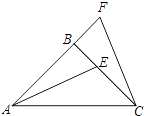 (1)、求证:△ABE≌△CBF;(2)、若∠BAE=25°,求∠ACF的度数.
(1)、求证:△ABE≌△CBF;(2)、若∠BAE=25°,求∠ACF的度数.
20. 如图,已知:在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D , BC=CE .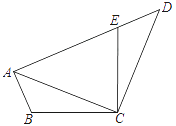 (1)、求证:AC=CD;(2)、若AC=AE , 求∠DEC的度数.21. 如图,在直角坐标系中,A、B、C、D各点的坐标分别为(﹣7,7)、(﹣7,1)、(﹣3,1)、
(1)、求证:AC=CD;(2)、若AC=AE , 求∠DEC的度数.21. 如图,在直角坐标系中,A、B、C、D各点的坐标分别为(﹣7,7)、(﹣7,1)、(﹣3,1)、(﹣1,4).
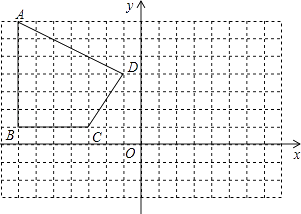 (1)、在给出的图形中,画出四边形ABCD关于y轴对称的四边形A1B1C1D1; (不写作法)(2)、写出点A1和C1的坐标;
(1)、在给出的图形中,画出四边形ABCD关于y轴对称的四边形A1B1C1D1; (不写作法)(2)、写出点A1和C1的坐标;
(3)、求四边形A1B1C1D1的面积.
22. 威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.(1)、求每件A种商品和每件B种商品售出后所得利润分别为多少元?(2)、由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?23. 如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.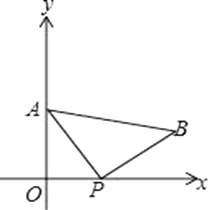
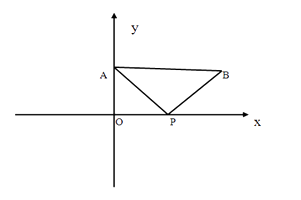 (1)、若AB//x轴,如图一,求t的值;
(1)、若AB//x轴,如图一,求t的值;
(2)、当t=3时,坐标平面内有一点M(不与A重合) , 使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标;
(3)、设点A关于x轴的对称点为 ,连接 ,在点P运动的过程中,∠ 的度数是否会发生变化,若不变,请求出∠ 的度数,若改变,请说明理由。