浙江宁波慈溪市2016届数学中考一模试卷

试卷更新日期：2018-01-08 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2016的倒数是（）

A、2016 B、-2016 C、 $\frac{1}{2016}$ D、 $- \frac{1}{2016}$

查看试题解析
2. 下列计算正确的是（）

A、(a²)³＝a⁵ B、2a－a＝2 C、(2a)²＝4a D、a·a³＝a⁴

查看试题解析
3. 宁波地铁1号线二期于2016年3月19日开通试运营，当天客流量超25万人次，数据25万用科学记数法表示为（）

A、2.5×10⁴ B、2.5×10⁵ C、0.25×10⁵ D、0.25×10⁶

查看试题解析
4. 不等式组 ${\begin{cases} - 2 x > 1 \\ x - 1 < 0 \end{cases}$ 的解集是（）

A、x＞﹣ $\frac{1}{2}$ B、x＜﹣ $\frac{1}{2}$ C、x＜1 D、﹣ $\frac{1}{2}$ ＜x＜1

查看试题解析
5. 在一次汉字听写大赛中，10名学生得分情况如表：
人数
3
4
2
1
分数
80
85
90
9595
那么这10名学生所得分数的中位数和众数分别是（）

A、85和82.5 B、85.5和85 C、85和85 D、85.5和80

查看试题解析
6. 如图所示的几何体是由一些正方体组合而成的立体图形，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
7. 用配方法解方程x²-4x+1=0时，配方后所得的方程是（）

A、(x-2)²=1 B、(x-2)²=-1 C、(x-2)²=3 D、(x+2)²=3

查看试题解析
8. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B＝135°，则 $\vec{A C}$ 的长为（）

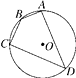A、2π B、π C、 $\frac{π}{2}$ D、 $\frac{π}{3}$

查看试题解析
9.
如图，在空白网格内将某一个小正方形涂成阴影部分，且所涂的小正方形与原阴影图形的小正方形至少有一边重合．小红按要求涂了一个正方形，所得到的阴影图形恰好是轴对称图形的概率为（　　）

A、 $\frac{1}{5}$ B、 $\frac{41}{15}$ C、 $\frac{4}{9}$ D、 $\frac{1}{3}$

查看试题解析
10. 在平面直角坐标系中，二次函数y=﹣x²+6x﹣9的图象顶点为A，与y轴交于点B．若在该二次函数图形上取一点C，在x轴上取一点D，使得四边形ABCD为平行四边形，则D点的坐标为（）

A、（﹣9，0） B、（﹣6，0） C、（6，0） D、（9，0）

查看试题解析
11. 如图，在△ABC、△ADE中，C、D两点分别在AE、AB上，BC、DE交于点F，若BD=DC=CE，∠ADC+∠ACD=114°，则∠DFC为（）

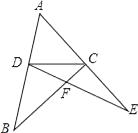A、114° B、123° C、132° D、147°

查看试题解析
12. 如图1是一张等腰直角三角形彩色纸，将斜边上的高线四等分，然后裁出三张宽度相等的长方形纸条，若恰好可以用这些纸条为一幅正方形美术作品镶边（纸条不重叠），则这张彩色纸的面积与镶嵌所得的作品（如图2）面积之比为（）

A、2：3 B、3：4 C、1：1 D、4：3

查看试题解析

二、填空题

13. 已知函数 $y = \frac{x - 1}{\sqrt{x} - 2}$ ，下列x的值：①x=﹣9；②x=0；③x=4：其中在自变量取值范围内的有（只要填序号即可）

查看试题解析
14. 已知直线y=kx+b经过点（2，3），则4k+2b﹣7= ．

查看试题解析
15. 一个不透明的布袋中，装有红、黄、白、黑四种只有颜色不同的小球，其中红色小球有30个，黄、白、黑色小球的数目相同．为估计袋中黄色小球的数目，每次将袋中小球搅匀后摸出一个小球记下颜色，放回后再次搅匀…多次试验发现摸到红球的频率是 $\frac{1}{3}$ ，则估计黄色小球的数目是．

查看试题解析
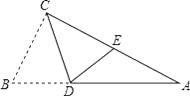
16. 如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处．若∠A=26°，则∠CDE= ．

查看试题解析
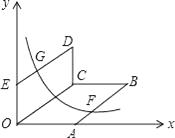
17. 如图，0为原点，A（4，0），E（0，3），四边形OABC，四边形OCDE都为平行四边形，OC=5，函数y= $\frac{k}{x}$ （x＞0）的图象经过AB的中点F和DE的中点G，则k的值为．

查看试题解析
18. 如图，A点的坐标是（0，6），AB=BO，∠ABO=120°，C在x轴上运动，在坐标平面内作点D，使AD=DC，∠ADC=120°，连结OD，则OD的长的最小值为．

查看试题解析

三、解答题

19. 计算：（﹣3）²+（ $\frac{1}{2016}$ ）⁰﹣ $\sqrt[3]{8}$ +2^﹣1+ $\sqrt{3}$ •tan30°．

查看试题解析
20. 先化简，再求值： $\frac{4}{x^{2} - 4} + \frac{1}{2 - x}$ ，其中x=﹣3．

查看试题解析
21. 中考英语听力测试期间_T需要杜绝考点周围的噪音．如图，点A是某市一中考考点，在位于考点南偏西15°方向距离500米的C点处有一消防队．在听力考试期间，消防队突然接到报警电话，消防车需沿北偏东75°方向的公路CF前往救援．已知消防车的警报声传播半径为400米，若消防车的警报声对听力测试造成影响，则消防车必须改道行驶．试问：消防车是否需要改道行驶？
说明理由．（ $\sqrt{3}$ ≈1.732）

查看试题解析
22. 如图，在平面直角坐标系中，一次函数y=ax﹣a（a为常数）的图象与y轴相交于点A，与函数y= $\frac{2}{x}$ 的图象相交于点B（m，1）．

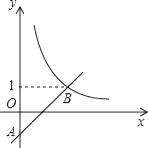(1)、求点B的坐标及一次函数的解析式；

(2)、若点P在y轴上，且△PAB为直角三角形，请直接写出点P的坐标．

查看试题解析
23. 垃圾的分类处理与回收利用，可以减少污染，节省资源．某城市环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况，其相关信息如图：
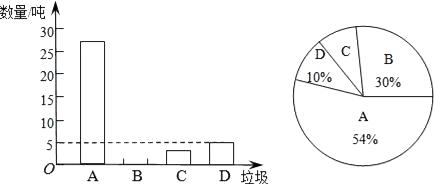
（注：A为可回收物，B为厨余垃圾，C为有害垃圾，D为其他垃圾）
根据图表解答下列问题：

(1)、在抽样数据中，产生的有害垃圾共多少吨？

(2)、请将条形统计图补充完整；

(3)、调查发现，在可回收物中塑料类垃圾占 $\frac{1}{2}$ ，每回收1吨塑料类垃圾可获得0.7吨二级原料．假设该城市每月产生的生活垃圾为5000吨，且全部分类处理，那么每月回收的塑料类垃圾可以获得多少吨二级原料？

查看试题解析
24. 我市某校准备组织学生及学生家长坐高铁到杭州进行社会实践，为了便于管理．所有人员必须乘坐在同一列高铁上．根据报名人数，若都买一等座单程火车票需6560元，若都买二等座单程火车票，则需3120元（学生票二等座打7.5折，一等座不打折）．已知学生家长与教师的人数之比为3：1，余姚北站到杭州东站的火车票价格如表所示：
运行区间
票价
上车站
下车站
一等座
二等座
余姚北
杭州东
82（元）
48（元）

(1)、参加社会实践的老师、家长与学生各有多少人？

(2)、由于各种原因，二等座火车票单程只能买m张（m小于参加社会实践的人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐的前提下，请你设计最经济的购票方案，并写出购买火车票的总费用（单程）y（元）（用含m的代数式表示）．

查看试题解析
25. 定义：圆心在三角形的一边上，与另一边相切，且经过三角形一个顶点（非切点）的圆，称为这个三角形圆心所在边上的“伴随圆”．

(1)、如图1，△ABC中，∠C=90°，AB=5，BC=3，则AC边上的伴随圆的半径为．

(2)、如图2，已知等腰△ABC，AB=AC=5，BC=6，画草图并直接写出它的所有伴随圆的半径．

(3)、如图3，△ABC中，∠ACB=90°，点P在边AB上，AP=2BP，D为AC中点，且∠CPD=90°．
①求证：△CPD的外接圆是△ABC某一条边上的伴随圆；
②求cos∠PDC的值．

查看试题解析
26. 如图，抛物线y=ax²+bx+3交x轴于A（﹣1，0）和B（5，0），交y轴于点C，点D是线段OB上一动点，连接CD，将CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴，垂足为H，过点C作CF⊥l于F，连接DF，CE交于点G．

(1)、求抛物线解析式；

(2)、求线段DF的长；

(3)、当DG= $\frac{5 \sqrt{2}}{3}$ 时，
①求tan∠CGD的值；
②试探究在x轴上方的抛物线上，是否存在点P，使∠EDP=45°？若存在，请写出点P的坐标；若不存在，请说明理由．

查看试题解析

运行区间		票价
上车站	下车站	一等座	二等座
余姚北	杭州东	82（元）	48（元）

人数	3	4	2	1
分数	80	85	90	9595