湖北省孝感市八校联谊2017-2018学年九年级上学期数学12月联考试卷
试卷更新日期:2018-01-06 类型:月考试卷
一、选择题
-
1. 下列图案中,是中心对称图形的是( )
 A、①② B、②③ C、②④ D、③④2. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断3. 抛物线 的顶点是( )
A、①② B、②③ C、②④ D、③④2. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断3. 抛物线 的顶点是( )
A、 B、 C、 D、4. 如图,在平面直角坐标系中,点 的坐标为 ,以原点 为中心,将点 逆时针旋转 得到点 ,则点 坐标为( ) A、 B、 C、 D、5. 将抛物线 向右平移 个单位,再向上平移 个单位,所得抛物线的函数表达式是( )
A、 B、 C、 D、5. 将抛物线 向右平移 个单位,再向上平移 个单位,所得抛物线的函数表达式是( )
A、 B、 C、 D、6. 如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50,则∠DAC的大小为( ) A、130 B、100 C、65 D、507. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为 ,则下面所列方程正确的是( )
A、130 B、100 C、65 D、507. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为 ,则下面所列方程正确的是( ) A、 B、 C、 D、8. 如图,在 中, ,以 的中点 为圆心分别与 , 相切于 , 两点,则 的长为( )
A、 B、 C、 D、8. 如图,在 中, ,以 的中点 为圆心分别与 , 相切于 , 两点,则 的长为( ) A、 B、 C、 D、9. 已知 整数,且满足 ,则关于 的一元二次方程 的解为( )A、 或 B、 C、 D、10. 二次函数 的图象如图,给出下列四个结论:① ;② ;
A、 B、 C、 D、9. 已知 整数,且满足 ,则关于 的一元二次方程 的解为( )A、 或 B、 C、 D、10. 二次函数 的图象如图,给出下列四个结论:① ;② ;③ ;④ ,其中正确结论的个数是( )
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 已知关于 的方程 的一个根为2,则另一个根是.
12. 若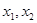 是方程 的两个实数根,且
是方程 的两个实数根,且 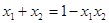 ,则 的值为.
,则 的值为.
13. 一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图的扇形的圆心角是.
14. 如图,将△AOB绕点O按逆时针方向旋转45后,得到△COD,如果∠AOB=15,则∠AOD的度数是. 15. 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45,若点M、N分别是AB、AC的中点,则MN长的最大值是.
15. 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45,若点M、N分别是AB、AC的中点,则MN长的最大值是. 16. 对称轴与 轴平行且经过原点O的抛物线也经过 ,若 的面积为4,则抛物线的解析式为.
16. 对称轴与 轴平行且经过原点O的抛物线也经过 ,若 的面积为4,则抛物线的解析式为.
三、解答题
-
17. 解下列方程:
(1)、
(2)、
18. 如图所示,在Rt△ABC中,∠ACB=90,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点按顺时针方向旋转90后得CE,连接EF. (1)、求证:△BCD≌△FCE;(2)、若EF∥CD,求∠BDC的度数.
(1)、求证:△BCD≌△FCE;(2)、若EF∥CD,求∠BDC的度数.
19. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度, 的三个顶点的坐标分别 (1)、画出 关于 轴的对称图形 ;(2)、画出将 绕原点 逆时针方向旋转 得到的 ;(3)、求(2)中线段 扫过的图形面积.
(1)、画出 关于 轴的对称图形 ;(2)、画出将 绕原点 逆时针方向旋转 得到的 ;(3)、求(2)中线段 扫过的图形面积.
20. 如图,已知在△ABC中,∠A=90 (1)、请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).(2)、若∠B=60,AB=3,求⊙P的面积.
(1)、请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).(2)、若∠B=60,AB=3,求⊙P的面积.
21. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在 点上正方 的 处发出一球,羽毛球飞行的高度 与水平距离 之间满足函数表达式 .已知点 与球网的水平距离为 ,球网的高度为 . (1)、当 时,①求 的值;
(1)、当 时,①求 的值;②通过计算判断此球能否过网;
(2)、若甲发球过网后,羽毛球飞行到 处时,乙扣球成功。已知点 离点 的水平距离为 ,离地面的高度为 的,求 的值.22. 已知关于 的一元二次方程 有两个实数根 .(1)、求 的取值范围;(2)、若 满足 ,求 的值.
23. 如图,在Rt△ABC中,∠ACB=90,以AC为直径作 交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F. (1)、求证:DE是 的切线;(2)、若CF=2,DF=4,求 直径的长.24. 如图,是将抛物线 平移后得到的抛物线,其对称轴为 ,与x轴的一个交点为A ,另一交点为B,与y轴交点为C.
(1)、求证:DE是 的切线;(2)、若CF=2,DF=4,求 直径的长.24. 如图,是将抛物线 平移后得到的抛物线,其对称轴为 ,与x轴的一个交点为A ,另一交点为B,与y轴交点为C. (1)、求抛物线的函数表达式;(2)、若点 N 为抛物线上一点,且BC⊥NC,求点N的坐标;(3)、点P是抛物线上一点,点Q是一次函数 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
(1)、求抛物线的函数表达式;(2)、若点 N 为抛物线上一点,且BC⊥NC,求点N的坐标;(3)、点P是抛物线上一点,点Q是一次函数 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.