湖北省孝感市八校联谊2017-2018学年八年级数学上学期12月联考试卷
试卷更新日期：2018-01-06 类型：月考试卷
一、选择题
-
1. 第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列运算正确的是（ ）A、－2(a+b)=－2a+2b B、(2b2)3=8b5 C、3a2•2a3=6a5 D、a6－a4=a23. 若一个多边形的内角和与它的外角和相等，则这个多边形是（ ）A、三角形 B、四边形 C、五边形 D、六边形4. 长为10，7，5，3的四根木条，选其中三根首尾顺次相连接组成三角形，选法有（ ）A、1种 B、2种 C、3种 D、4种5. 如图，已知AB=AD，添加一个条件后，仍然不能判定△ABC≌△ADC的是（ ）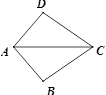
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°6. 如图，在等边△ABC中，BD平分∠ABC交AC于点D，过点D作DE⊥BC于点E，且CE=2，则AB的长为（ ）
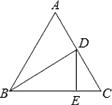A、8 B、4 C、6 D、7.57. 如图，由4个小正方形组成的田字格中，△ABC的顶点都是小正方形的顶点，在田字格上画与△ABC成轴对称的三角形，且顶点都是小正方形的顶点，则这样的三角形的个数有(不包含△ABC本身)（ ）
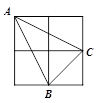A、4个 B、3个 C、2个 D、1个8. 两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积= AC•BD，其中正确的结论有（ ）
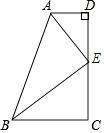
A、①② B、①③ C、②③ D、①③②9.如图，∠D=∠C=90°，E是DC的中点，AE平分∠DAB，∠DEA=28°，则∠ABE的度数是（ ）
A、62 B、31 C、28 D、2510. 如图△ABC与△CDE都是等边三角形，且∠EBD=65°，则∠AEB的度数是（ ）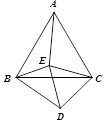
A、115° B、120° C、125° D、130°二、填空题
-
11. 计算（2m2n2）2•3m2n3的结果是 ．
12. 如图，三角形纸片ABC，AB=11cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为cm．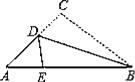
13. 点M（－5，3）关于x轴对称的点N的坐标是 ．
14. 如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中阴影部分的面积S是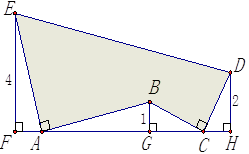
15. 如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于D点．若BD平分∠ABC，则∠A=°．
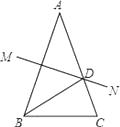16. 如图，△ABC中，线段BC的垂直平分线DP与∠BAC的角平分线相交于点D，垂足为点P，若∠BAC=84°，则∠BDC= °．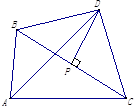
三、解答题
-
17. 如图，将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后，得到∠1＋∠2＋∠3＋∠4＋∠5＝400°，求∠BGD的度数．
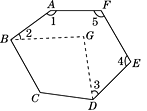18. 如图，点E，C在BF上，BE=CF，AB=DF，∠B=∠F．求证：∠A=∠D．
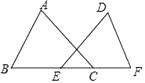19. 计算：(1)、6mn2·(2－mn4)＋(－mn3)2；
(2)、 (1＋a)(1－a)＋(a－2)2(3)、(x＋2y)2－(x－2y)2－(x＋2y)(x－2y)－4y2 ， 其中x＝－2，y＝.20. 已知等腰三角形的三边长分别为a+1，2a，5a－2，求这个等腰三角形的周长．
21. 如图所示，△ABC的顶点分别为A（-4， 5），B（﹣3， 2），C（4，-1）．
(1)、作出△ABC关于x轴对称的图形△A1B1C1；(2)、写出A1、B1、C1的坐标；(3)、若AC=10，求△ABC的AC边上的高．22. 如图，△ABC中， ∠BAC=∠ADB，BE平分∠ABC交AD于点E，H为BC上一点，且BH=BA交AC于点F，连接FH.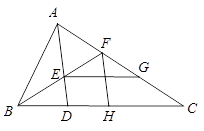
(1)、求证：AE=FH；(2)、作EG//BC交AC于点G若AG=5，AC=8，求FG的长.
23.
(1)、 已知：如图1，等腰直角三角形ABC中，∠B=90°，AD是∠BAC的外角平分线，交CB边的延长线于点D．
求证：BD=AB+AC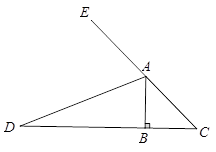
图1
(2)、对于任意三角形ABC，∠ABC=2∠C，AD是∠BAC的外角平分线，交CB边的延长线于点D，如图2，请你写出线段AC、AB、BD之间的数量关系并加以证明．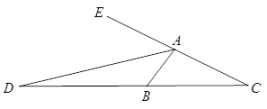
24. 如图，△ABC中，∠ABC=∠ACB，点D在BC所在的直线上，点E在射线AC上，且AD=AE，连接DE．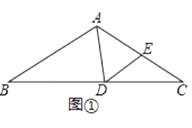
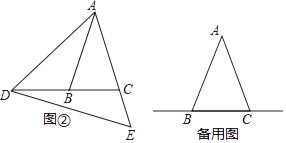
(1)、如图①，若∠B=∠C=35°，∠BAD=80°，求∠CDE的度数；
(2)、如图②，若∠ABC=∠ACB=75°，∠CDE=18°，求∠BAD的度数；
(3)、当点D在直线BC上（不与点B、C重合）运动时，试探究∠BAD与∠CDE的数量关系，并说明理由．