广东省广州市海珠区2015-2016学年七年级上学期数学期末考试试卷
试卷更新日期:2017-12-29 类型:期末考试
一、单选题
-
1. ﹣2的相反数是( )A、2 B、﹣2 C、±2 D、2. 如图,矩形绕它的一条边MN所在的直线旋转一周形成的几何体是( )
 A、
A、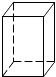 B、
B、 C、
C、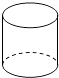 D、
D、 3. 下列方程组中是二元一次方程组的是( )
3. 下列方程组中是二元一次方程组的是( )
A、 B、 C、 D、4. 下列运用等式性质进行的变形,其中不正确的是( )A、如果a=b,那么a+3=b+3 B、如果a=b,那么a﹣=b﹣ C、如果a=b,那么ac=bc D、如果a=b,那么5. 如图,点A位于点O的( )方向上. A、西偏东35° B、北偏西65° C、南偏东65° D、南偏西65°6. 下列选项中,是方程x﹣2y=2的解是( )
A、西偏东35° B、北偏西65° C、南偏东65° D、南偏西65°6. 下列选项中,是方程x﹣2y=2的解是( )
A、 B、 C、 D、7. 解方程 时,去分母后,正确的是( )
A、3x﹣2(x﹣1)=1 B、2x﹣3(x﹣1)=1 C、3x﹣2(x﹣1)=6 D、2x﹣3(x﹣1)=68. 下列图形不能围成正方体的是( )
A、 B、
B、 C、
C、 D、
D、 9. 设有理数a、b在数轴上对应的位置如图所示,化简|a﹣b|﹣|a|的结果是( )
9. 设有理数a、b在数轴上对应的位置如图所示,化简|a﹣b|﹣|a|的结果是( )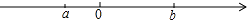 A、﹣2a+b B、2a+b C、﹣b D、b10. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“
A、﹣2a+b B、2a+b C、﹣b D、b10. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( ) A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b
A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b二、填空题
-
11. 在﹣2、0、1、﹣1这四个数中,最大的有理数是 .
12. 据数据显示,2015年某电商的“双十一”全球狂欢节最终以约91200000000元交易额落下帷幕!将91200000000用科学记数法表示为 .13. 若﹣5x2ym与x2y是同类项,m= .14. 一个角的余角是这个角的4倍,则这个角的度数是 .15. 如图,直线AB,CD相交于点O,∠AOD=3∠BOD+20°,则∠BOD= . 16. 一组按规律排列的式子: 则第1008个式子是 .
16. 一组按规律排列的式子: 则第1008个式子是 .
三、解答题
-
17. 计算
(1)、(+16)﹣(﹣7)﹣(+11)(2)、(﹣3)2×2﹣(﹣4)÷2.18. 解方程或方程组:
(1)、5x+5=9﹣3x;(2)、 .19. 先化简,再求值3(x2﹣2y)﹣2(x2﹣2y),其中x=﹣1,y=2.20. 某机械厂加工车间有84名工人,平均每人每天加工大齿轮16个或者小齿轮10个,已知1个大齿轮与2个小齿轮刚好配成一套,问分别安排多少名工人加工大,小齿轮,才能使每天加工的大小齿轮刚好配套?21. 点A、B、C在同一条直线上,AB=6cm,BC=2cm,点M是线段AC的中点,求AM的长.
22. 出租车司机小李某天上午从家出发,营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:km)如下:-1,+6,-2,+2,-7,-4.(1)、将最后一位乘客送到目的地时,小李在出发地的哪一边?距离出发地多少km?(2)、若汽车每千米耗油量为0.2升,这天上午小李接送乘客,出租车共耗油多少升?23. 某城市自来水收费实行阶梯水价,收费标准如下表所示: (1)、某用户四月份用水量为16吨,需交水费为多少元?(2)、某用户五月份交水费50元,所用水量为多少吨?(3)、某用户六月份用水量为a吨,需要交水费为多少元?24. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
(1)、某用户四月份用水量为16吨,需交水费为多少元?(2)、某用户五月份交水费50元,所用水量为多少吨?(3)、某用户六月份用水量为a吨,需要交水费为多少元?24. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.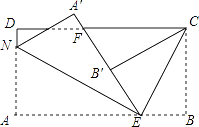 (1)、若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.(2)、若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.(3)、将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.25. A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.(1)、若2秒后,a、b满足|a+8|+(b﹣2)2=0,则x= , y= , 并请在数轴上标出A、B两点的位置.(2)、若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .(3)、若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .
(1)、若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.(2)、若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.(3)、将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.25. A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.(1)、若2秒后,a、b满足|a+8|+(b﹣2)2=0,则x= , y= , 并请在数轴上标出A、B两点的位置.(2)、若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .(3)、若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .