河南省平顶山市宝丰县2016届九年级上学期数学期末考试试卷
试卷更新日期:2017-12-29 类型:期末考试
一、单选题
-
1. sin30°=( )A、0 B、1 C、 D、2. 一元二次方程x2﹣2x=0的根是( )A、x1=0,x2=﹣2 B、x1=1,x2=2 C、x1=1,x2=﹣2 D、x1=0,x2=23.
如图所示的物体的左视图为( )
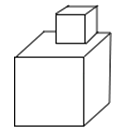 A、
A、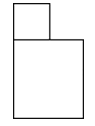 B、
B、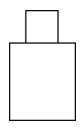 C、
C、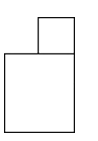 D、
D、 4. 在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
4. 在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
A、y=3(x+1)2+2 B、y=3(x+1)2﹣2 C、y=3(x﹣1)2+2 D、y=3(x﹣1)2﹣25. 一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,求这张卡片与口袋外的两张卡片上的数能构成三角形的概率是( )
A、 B、 C、 D、16. 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A、﹣11 B、﹣2 C、1 D、﹣57. 如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )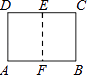 A、2:1 B、 :1 C、3: D、3:28. 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A、2:1 B、 :1 C、3: D、3:28. 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )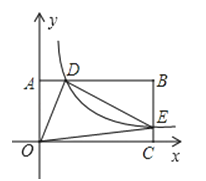 A、 B、 C、 D、129. 抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
A、 B、 C、 D、129. 抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:①abc>0;
②a+b>0;
③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤若c≤﹣1,则b2﹣4ac≤4a.
其中结论错误的是 . (只填写序号)
二、填空题
-
10. 抛物线y=3(x﹣2)2+5的顶点坐标是 .11. 已知正六边形的周长是12,则它的半径是 .
12. 关于x的一元二次方程x2﹣3x+k=0有两个不相等的实数根,则k的取值范围是 .
13. 已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们的两个交点的横坐标是1和4,那么能够使得y1<y2的自变量x的取值范围是 .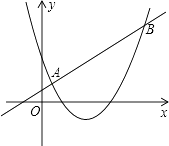 14. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 cm,∠BCD=22°30′,则⊙O的半径为cm.
14. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 cm,∠BCD=22°30′,则⊙O的半径为cm.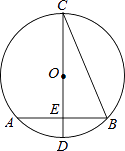 15. 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1: ,点A的坐标为(0,1),则点E的坐标是 .
15. 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1: ,点A的坐标为(0,1),则点E的坐标是 .
三、解答题
-
16. 已知关于x的方程x2+ax+a﹣2=0
(1)、若该方程的一个根为1,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程总有两个不相等的实数根
17. 如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4 ,求⊙O的半径.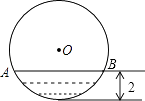 18. 如图,一次函数y=kx+b与反比例函数y= (x>0)的图象交于A(m,6),B(3,n)两点.
18. 如图,一次函数y=kx+b与反比例函数y= (x>0)的图象交于A(m,6),B(3,n)两点.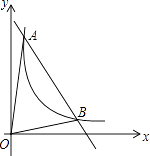 (1)、求一次函数的解析式;(2)、根据图象直接写出使kx+b< 成立的x的取值范围;(3)、求△AOB的面积.19. 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
(1)、求一次函数的解析式;(2)、根据图象直接写出使kx+b< 成立的x的取值范围;(3)、求△AOB的面积.19. 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).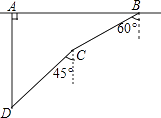 20. 如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
20. 如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.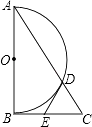 (1)、求证:DE是半圆⊙O的切线.
(1)、求证:DE是半圆⊙O的切线.
(2)、若∠BAC=30°,DE=2,求AD的长.
21. 永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价)
(1)、写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)、当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元?(3)、物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元?
22. 二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣ x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).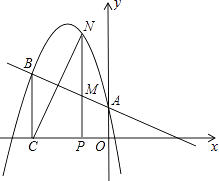 (1)、求二次函数的表达式;(2)、点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;(3)、在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
(1)、求二次函数的表达式;(2)、点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;(3)、在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.