广东省肇庆市四中2016届九年级上学期数学期末考试试卷
试卷更新日期：2017-12-29 类型：期末考试
一、单选题
-
1. 函数y=（x+1）2-2的最小值是（ ）
A、1 B、－1 C、2 D、－22. 方程x（x-2）=0的根为：（ ）A、1 B、0 C、2 D、2和03. 将抛物线y=3x2先向上平移3个单位，再向左平移2个单位后得到的抛物线解析式为：（ ）A、y=3（x+2）2+3 B、y=3（x-2）2+3 C、y=3（x+2）2-3 D、y=3（x-2）2-34. 某种型号的电视机经过连续两次降价，每台售价由原来的1500元，降到了980元，设平均每次降价的百分率为x，则下列方程中正确的是：（ ）
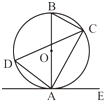
A、1500（1-x）2=980 B、1500（1+x）2=980 C、980（1-x）2=1500 D、980（1+x）2=15005. 如图、四边形 ABCD内接于⊙O，若∠BOD=100°，则∠DCB的度数为：（ ）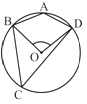
A、50° B、80° C、100° D、130°6. 已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根，则a的值是：（ ）
A、4 B、-4 C、1 D、-17. 从1、2、3、4、5、6、7、8、9、10这十个数中随机取出一个数，取出的数是3的倍数的概率是：（ ）
A、 B、 C、 D、8. 如图，AB为圆O的直径，弦CD⊥AB，垂足为点E，连结OC，若OC=5，CD=8，则AE的长是：（ ）
A、4 B、2 C、1 D、39. 如图，抛物线y=ax2+bx+c（a≠0）经过点（-1，0），对称轴为：直线x=1，则下列结论中正确的是：（ ）
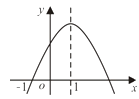A、a＞0 B、当x＞1时，y随x的增大而增大 C、
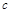＜0
D、x=3是一元二次方程ax2+bx+c=0（a≠0）的一个根
10. 将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1．在图2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．若骰子的初始位置为图1所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是：（ ）
A、6 B、5 C、3 D、2二、填空题
-
11. 方程x 2-5x-6=0的解是 ．12. 如图，A、B、C是⊙O上的三个点，∠ABC=25°，则∠AOC的度数是 ．
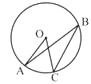13. 如图，PA、PB分别切⊙O于A、B两点，∠APB＝50°，则∠AOP＝ ．
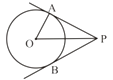14. 如图所示，抛物线y=ax2+bx+c（a≠0）与x轴的两个交点分别为A（-2，0）和B（6，0），当y＜0时，x的取值范围是 ．
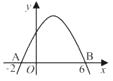15. 已知抛物线y=ax2+bx+c（a＞0）的对称轴为直线
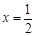，且经过点（-3，y1），（4，y2），试比较y1和y2的大小：y1y2（填“＞”，“＜”或“＝”）．
16. 如图，Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的，且A、O、B1三点共线．如果∠OAB=90°，∠AOB=30°，OA= ．则图中阴影部分的面积为 ． （结果保留π）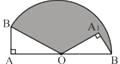
三、解答题
-
17. 如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC＝110°．连接AC，求∠A的度数．
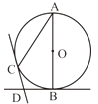18. 一个不透明的口袋里装有红、白、黄三种颜色的乒乓球（除颜色外其余都相同），其中有白球2个，黄球1个．若从中任意摸出一个球，这个球是白球的概率为0.5．
(1)、求口袋中红球的个数．
(2)、小明认为口袋中共有三种颜色的球，所以从袋中任意摸出一球，摸到红球、白球或黄球的概率都是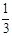
，你认为对吗?请你用列表或画树状图的方法说明理由．
19. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在格点上，在建立平面直角坐标系后，点A的坐标为（-6，1），点B的坐标为（-3，1），点C的坐标为（-3，3）．将Rt△ABC绕点B顺时针旋转90°得到Rt△A1B1C1 ， 试在图上画出的图形Rt△A1B1C1的图形，并写出点A1 ， C1的坐标；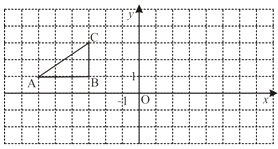
20. 如图，二次函数的图象与x轴交于A（-3，0）和B（1，0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．
(1)、求二次函数的解析式；(2)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围；
