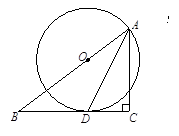广东省肇庆市端州区2016届九年级上学期数学期末考试试卷A卷
试卷更新日期：2017-12-29 类型：期末考试
一、单选题
-
1. 若一元二次方程ax2+bx+c=0有一根为0，则下列结论正确的是（ ）A、a=0 B、b=0 C、c=0 D、c≠02. 下列图案中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 关于抛物线y=(x-1)2-2，下列说法中错误的是（ ）
A、顶点坐标为(1，-2) B、对称轴是直线x=1 C、当x＞1时，y随x的增大而减小 D、开口方向向上4. 如图，∠A是⊙O的圆周角，∠A=50°，则∠BOC的度数为（ ）
A、40° B、50° C、90° D、100°5. 下列事件中是必然事件的是（ ）A、实心铁球投入水中会沉入水底 B、抛出一枚硬币，落地后正面向上 C、明天太阳从西边升起 D、NBA篮球队员在罚球线投篮2次，至少投中一次6. 用配方法解方程x2-4x+2=0，下列配方正确的是：（ ）
A、(x-1)2=-2 B、(x-2)2=2 C、(x+2)2=2 D、(x-2)2=67. 下列说法正确的是（ ）A、三点确定一个圆 B、平分弦的直径垂直于弦，并且平分弦所对的两条弧 C、与直径垂直的直线是圆的切线 D、能够互相重合的弧是等弧8. 如图，AB是⊙O的弦，半径OC⊥AB于点D，且AB=6cm，OD=4cm。则DC的长为（ ）
A、 cm B、1cm C、2cm D、5cm9. 若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根，则k的取值范围是（ ）
A、k＞ B、k≥ C、k＞ 且k≠1 D、k≥ 且k≠110. 二次函数y=ax2+bx+c的图像如图所示，则①abc；②b2-4ac；③2a+b；④a+b+c这四个式子中，值为负数的有个（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若x1、x2是一元二次方程x2-3x-1=0的两个根，则x1+x2的值是。
12. 在平面直角坐标系中，点P(1，-5)关于原点对称点P′的坐标是。13. 把抛物线y=2x2先向左平移3个单位，再向下平移4个单位，所得的抛物线的解析式是。
14. 正六边形的边长为10cm，那么它的边心距等于cm
15. 在一个不透明的布袋中装有2个白球和n个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到黄球的概率是
，则n=。
三、解答题
-
16. 如图，把一副三角板如图（1）放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=4，CD=5。把三角板DCE绕着点C顺时针旋转15°得到△D1CE1（如图2），此时AB与CD1交于点O，则线段AD1的长度为。
17. 解方程：x2+7x+12=0。
18. 已知抛物线的顶点坐标为(-2，-3)，且经过点(-3，-2)，求这个抛物线的解析式。
19.已知：如图，C，D是以AB为直径的⊙O上的两点，且OD∥BC．求证：AD=DC．
20. 随着市民环保意识的增强，节庆期间烟花爆竹销售量逐年下降．某市2012年销售烟花爆竹20万箱，到2014年烟花爆竹销售量为9.8万箱．求该市2012年到2014年烟花爆竹年销售量的平均下降率．
21. 如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A (3，2)、B(1，3)。△AOB绕点O 逆时针旋转90°后得到△A1OB1.
(1)、画出旋转后的图形；
(2)、求线段OB在旋转过程中所扫过的图形面积（写过程）。
22. 甲、乙、丙、丁四位同学进行一次乒乓球单打比赛，要从中选出两位同学打第一场比赛．
(1)、请用树状图法或列表法，求恰好选中甲、丙两位同学的概率；(2)、若已确定甲打第一场，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率。
