浙江省临安市於潜二中2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期：2017-12-29 类型：期末考试
一、单选题
-
1. 已知点P的坐标为(1，-2)，则点P所在的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列图形是轴对称图形的是（ ）A、
B、
C、
D、
3. 若a＜b，则下列各式中一定成立的是（）A、a+2＞b+2 B、a-2＞b-2 C、-2a＞-2b D、 ＞4. 若点A（x1 ， y1）和点B（x2 ， y2）在正比例函数y=-3x的图象上，当x1＜x2时，y1与y2的大小关系为（ ）
A、y1＞y2 B、y1＜y2 C、y1=y2 D、y1与y2的大小不一定5. 如图所示，A，B，C分别表示三个村庄，AB=1000米，BC=600米，AC=800米，在社会主义新农村建设中，为了丰富群众生活，拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P的位置应在（ ）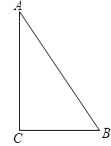
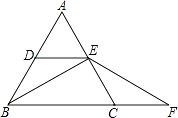
A、AB中点 B、BC中点 C、AC中点 D、∠C的平分线与AB的交点6. 如图，A，B，C三人的位置在同一直线上，AB=5米，BC=10米，下列说法正确的是（ ）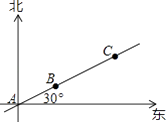
A、C在A的北偏东30°方向的15米处 B、A在C的北偏东60°方向的15米处 C、C在B的北偏东60°方向的10米处 D、B在A的北偏东30°方向的5米处7. 下列判断正确的是（ ）A、有一条直角边对应相等的两个直角三角形全等 B、腰长相等的两个等腰三角形全等 C、斜边相等的两个等腰直角三角形全等 D、两个锐角对应相等的两个直角三角形全等8. 如图，CE是△ABC的角平分线，EF∥BC，交AC于点F．已知∠AFE=64°，则∠FEC的度数为（ ）
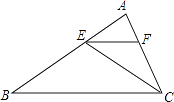A、64° B、32° C、36 D、26°9. 若方程组 的解x，y满足0＜x+y＜1，则k的取值范围是（ ）
A、-4＜k＜0 B、-1＜k＜0 C、0＜k＜8 D、k＞-410. 已知A，B两地相距40千米，中午12：00时，甲从A地出发开车到B地，12：10时乙从B地出发骑自行车到A地，设甲行驶的时间为t（分），甲、乙两人离A地的距离S（千米）与时间t（分）之间的关系如图所示．由图中的信息可知，乙到达A地的时间为（ ）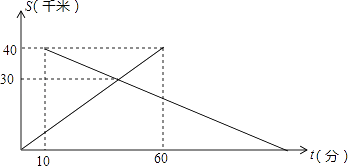
A、14：00 B、14：20 C、14：30 D、14：40二、填空题
-
11. 在Rt△ABC中，∠C=90°，∠A=25°，则∠B的度数为 ．
12. 用不等式表示：a与b的和不大于1．.
13. 命题“对顶角相等”的逆命题为 ．14. 已知点A（2，-3）与点B（a，-3）关于y轴对称，则a的值为 ．
15. 等腰三角形的两边长分别为2和4，则其周长为 ．
16. 已知y=2x+7，当-2＜x＜1时，y的取值范围为 ．
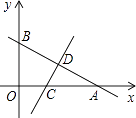
17. 已知Rt△ABC中，AB=3，AC=4，则BC的长为 ．18. 如图，已知点A（1，1），B（4，1），则线段AB上任意一点的坐标可表示为 ．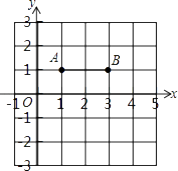
19. 如图，已知D，E是△ABC中BC边上的两点，且AD=AE，请你再添加一个条件：，使△ABD≌△ACE．
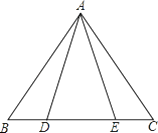20. 在平面直角坐标系xOy中，有一个边长为2个单位长度的等边△ABC，满足AC∥y轴．平移△ABC得到△A′B′C′，使点A′、B′分别在x轴、y轴上（不包括原点），则此时点C′的坐标是．.
三、解答题
-
21. 解不等式7x-2≤9x+2，把解集表示在数轴上，并求出不等式的负整数解．
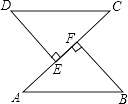
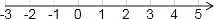22. 如图，已知AB=CD，DE⊥AC，BF⊥AC，垂足分别是点E，F，AE=CF．求证：AB∥CD．
23. 如图，已知∠BAC，用直尺和圆规作图：
①作∠BAC的平分线；
②在∠BAC的平分线上作点M，使点M到P、Q两点的距离相等．（不写作法，保留作图痕迹）
24. 某校有3名教师准备带领部分学生（不少于3人）参观植物园，经洽谈，植物园的门票价格为：教师票每张25元，学生票每张15元，且有两种购票优惠方案，方案一：购买一张教师票赠送一张学生票；方案二：按全部师生门票总价的80%付款．假如学生人数为x（人），师生门票总金额为y（元）．(1)、分别写出两种优惠方案中y与x的函数表达式；(2)、请通过计算回答，选择哪种购票方案师生门票总费用较少？
