河南省驻马店市2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2017-12-29 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{2 x}{x + 3}$ 有意义，则x的取值应满足（）

A、x=0 B、x≠0 C、x=﹣3 D、x≠﹣3

查看试题解析
2. 下列计算正确的是（　　）

A、a²•a³=a⁶ B、（﹣2ab）²=4a²b² C、（a²）³=a⁵ D、3a³b²÷a²b²=3ab

查看试题解析
3. 下面所给的图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）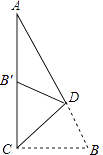

A、25° B、30° C、35° D、40°

查看试题解析
5. 下列因式分解错误的是（　　）

A、2a³﹣8a²+12a=2a（a²﹣4a+6） B、x²﹣5x+6=（x﹣2）（x﹣3） C、（a﹣b）²﹣c²=（a﹣b+c）（a﹣b﹣c） D、﹣2a²+4a﹣2=2（a+1）²

查看试题解析
6. 如图1是玩具拼图模板的一部分，已知△ABC的六个元素，则图2中甲、乙、丙三个三角形中能和△ABC完全重合的是（）

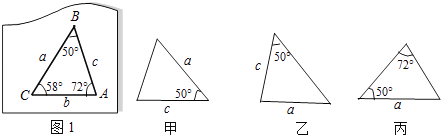A、甲和丙 B、丙和乙 C、只有甲 D、只有丙

查看试题解析
7. 如图，△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB，DE⊥AB于点E，连接CE交AD于点H，则图中的等腰三角形有（）

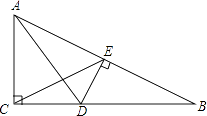A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

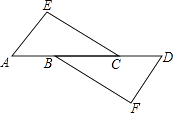
8. 计算：3^﹣2+（π﹣3）⁰﹣（﹣ $\frac{1}{3}$ ）²= ．

查看试题解析
9. 如图，AE∥FD，AE=FD，要使△EAC≌△FDB，则应补充条件（填写一个即可）．

查看试题解析
10. 如果x²+kx+81是一个完全平方式，那么k的值为．

查看试题解析
11. 若a=2b≠0，则 $\frac{a^{2} - b^{2}}{a^{2} - a b}$ 的值为．

查看试题解析
12. 如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD的度数是．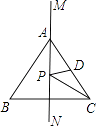

查看试题解析
13. 如图，已知∠AOB=60°，点P在边OA上，OP=12，点M，N在边OB上，PM=PN，若MN=2，则OM= ．

查看试题解析
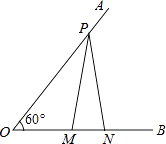14. 等腰三角形一腰上的高与另一腰的夹角为36°，则该等腰三角形的底角的度数为.

查看试题解析

三、解答题

15. 先化简，再求值：（x+2）²+（2x+1）（2x﹣1）﹣4x（x+1），其中x=﹣ $\sqrt{5}$ ．

查看试题解析
16. 小明化简（ $\frac{a + 2}{a^{2} - 2 a}$ ﹣ $\frac{a - 1}{a^{2} - 4 a + 4}$ ）÷ $\frac{a - 4}{a}$ 后说：“在原分式有意义的前提下，分式的值一定是正数”，你同意小明的说法吗？请说明理由．

查看试题解析
17. 如图，AB=AC，BD=DC，DE⊥AB，DF⊥AC，垂足分别是E，F．求证：DE=DF．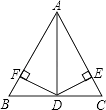

查看试题解析
18. 请阅读下列材料并回答问题：
在解分式方程 $\frac{2}{x + 1} - \frac{3}{x - 1} = \frac{1}{x^{2} - 1}$ 时，小明的解法如下：
解：方程两边同乘以（x+1）（x﹣1），得2（x﹣1）﹣3=1①
去括号，得2x﹣1=3﹣1 ②
解得x= $\frac{5}{2}$
检验：当x= $\frac{5}{2}$ 时，（x+1）（x﹣1）≠0 ③
所以x= $\frac{5}{2}$ 是原分式方程的解 ④

(1)、你认为小明在哪里出现了错误（只填序号）

(2)、针对小明解分式方程出现的错误和解分式方程中的其他重要步骤，请你提出三条解分式方程时的注意事项；

(3)、写出上述分式方程的正确解法．

查看试题解析
19. 列方程或方程组解应用题：
某园林队计划由6名工人对180平方米的区域进行绿化，由于施工时增加了2名工人，结果比计划提前3小时完成任务，若每人每小时绿化面积相同，求每人每小时的绿化面积．

查看试题解析
20. 如图，已知△ABC．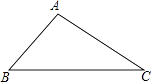

(1)、利用直尺和圆规，按照下列要求作图（保留作图痕迹，不要求写作法）
①作∠ABC的平分线BD交AC于点D；
②作线段BD的垂直平分线分别交AB、BC于点E、F．

(2)、连接DE，请判断线段DE与线段BF的数量关系，并说明理由．

查看试题解析
21. 小丽同学要画∠AOB的平分线，却没有量角器和圆规，于是她用三角尺按下面方法画角平分线：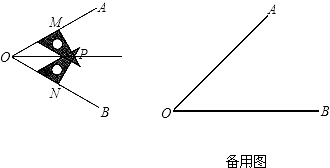
①在∠AOB的两边上，分别取OM=ON；
②分别过点M、N作OA、OB的垂线，交点为P；
③画射线OP，则OP为∠AOB的平分线．

(1)、请问：小丽的画法正确吗？试证明你的结论；

(2)、如果你现在只有刻度尺，能否画一个角的角平分线？请你在备用图中试一试．（不需要写作法，但是要让读者看懂，你可以在图中标明数据）

查看试题解析
22. 综合题

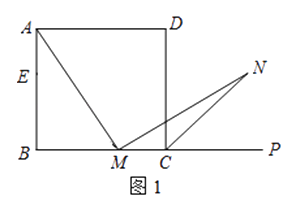
(1)、如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连接ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE．
（下面请你完成余下的证明过程）

(2)、若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则∠AMN=60°时，结论AM=MN是否还成立？请说明理由．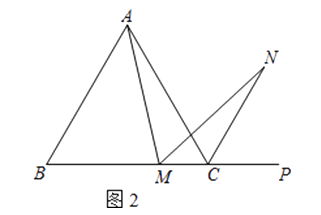

(3)、若将（1）中的“正方形ABCD”改为“正n边形ABCD…X，请你作出猜想：当∠AMN=时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

查看试题解析