河南省开封市通许县2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期：2017-12-29 类型：期末考试
一、单选题
-
1. 4的平方根是（ ）A、2 B、 C、±2 D、±2. （a2）4等于（ ）A、2a4 B、4a2 C、a8 D、a63. 如果（x+a）（x+b）的积中不含x的一次项，那么a，b一定（ ）
A、互为倒数 B、互为相反数 C、a=b且b=0 D、ab=04. 若x=﹣2n ， y=﹣3+4n ， 则x，y的关系是（ ）
A、y+3=x2 B、y﹣3=x2 C、3y=x2 D、﹣3y=x25. 下列命题正确的是（ ）A、若a＞b，b＜c，则a＞c B、若a＞b，则ac＞bc C、若a＞b，则ac2＞bc2 D、若ac2＞bc2 ， 则a＞b6. 如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（ ）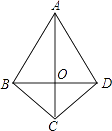
A、1对 B、2对 C、3对 D、4对7. 已知一个等腰三角形两内角的度数之比为1：4，则这个等腰三角形顶角的度数为（ ）A、20°或100° B、120° C、20°或120° D、36°8. 已知a，b，c为△ABC三边长，且满足a2+b2+c2=10a+6b+8c﹣50，则此三角形的形状为（ ）A、锐角三角形 B、等腰三角形 C、钝角三角形 D、直角三角形9. 若多项式x2+ax+9恰好是另一个多项式的平方，则a值（ ）A、±6 B、﹣6 C、3 D、±310. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（ ）
A、90° B、60° C、45° D、30°二、填空题
-
11. 计算： ﹣ = ．12. 已知am=2，an=3，则a2m﹣3n=.13. 如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是 ．
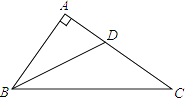14. 如图，在△ABC中，∠BAC=90°，AB=3，AC=4，AD平分∠BAC交BC于D，则BD的长为 ．
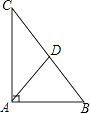15. 已知正方形面积a2﹣2ab﹣3b2（b＜0，a＞|b|）且它的一边长为a+b，则另一边用代数式表示 ．
16. 等边三角形的一条中线长为 ，则这个三角形边长等于 ．
17. 在△ABC中，AB=BC，AD平分∠BAC，AE=AB，△CDE的周长为8cm，那么AC长 ．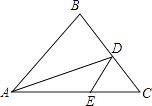
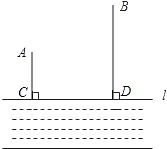
18. 如图，∠A=∠OCD=90°，OA=2，OD= ，AB=BC=CD=1，则△OBC形状 ．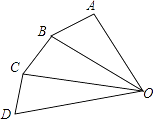
19. 已知|x|=1，|y|= ，则（x20）3﹣x3y2= ．20. 如图，在△ABC中，AD⊥BC且BD＞CD，DF⊥AB，△CDE和△ADB都是等腰直角三角形，给出下列结论，正确的是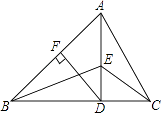
①△ADC≌△BDE；
②△ADF≌△BDF；
③△CDE≌△AFD；
④△ACE≌ABE．
三、解答题
-
21. 分解因式
①﹣a2+2ab﹣b2
②x2y﹣2xy2+xy
③16x4﹣72x2+81
④（a﹣b）3c﹣2（a﹣b）2c+（a﹣b）c．
22. 先化简，再求值：
(1)、[2x2﹣（x+y）（x﹣y）][（x﹣y）（y﹣x）﹣2xy]，其中x=1，y=2(2)、已知x2+x﹣6=0，求代数式x2（x+1）﹣x（x2﹣1）﹣7的值．23. 某中学了解本校学生对球类运动的爱好情况，分为足球、篮球、排球、其他四个方面调查若干名学生，每人只选其中之一，统计后绘制成不完整的“折线统计图”（扇形统计图），根据信息解答下列问题：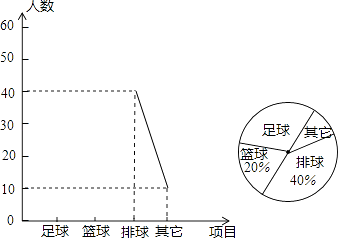
(1)、在这次调查中，一共调查名学生；
(2)、在扇形统计图中，“足球”所在扇形圆心角度；(3)、将折线统计图补充完整．24. 如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边三角形CDE，使点E，A在直线DC同侧，连接AE．求证：
(1)、△AEC≌△BDC；(2)、AE∥BC．25. 如图，某沿海开放城市A接到台风警报，在该市正南方向100km的B处有一台风中心，沿BC方向以20km/h的速度向D移动，已知城市A到BC的距离AD=60km，那么台风中心经过多长时间从B点移到D点？如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险，正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险？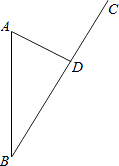
26. 如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少？