2017-2018学年人教版九年级上册数学第二十二章 二次函数 单元复习
试卷更新日期:2017-12-29 类型:单元试卷
一、单选题
-
1. 若抛物线y=(m﹣1)x 开口向下,则m的取值是( )A、﹣1或2 B、1或﹣2 C、2 D、﹣12. 对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1 , y2=﹣x22+2x2 , 则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为( )A、1 B、2 C、3 D、43.
二次函数y=ax2+bx+c的图象如图所示,则下列关系式不正确的是( )
 A、a<0 B、abc>0 C、a+b+c>0 D、b2-4ac>04. 在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )A、
A、a<0 B、abc>0 C、a+b+c>0 D、b2-4ac>04. 在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )A、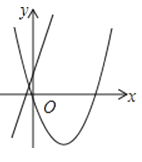 B、
B、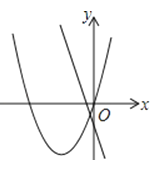 C、
C、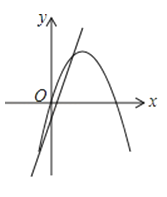 D、
D、 5.
5.如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
 A、b2>4ac B、ax2+bx+c≥﹣6 C、若点(﹣2,m),(﹣5,n)在抛物线上,则m>n D、关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣16. 直线y=ax﹣6与抛物线y=x2﹣4x+3只有一个交点,则a的值为( )A、a=2 B、a=10 C、a=2或a=﹣10 D、a=2或a=107. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、
A、b2>4ac B、ax2+bx+c≥﹣6 C、若点(﹣2,m),(﹣5,n)在抛物线上,则m>n D、关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣16. 直线y=ax﹣6与抛物线y=x2﹣4x+3只有一个交点,则a的值为( )A、a=2 B、a=10 C、a=2或a=﹣10 D、a=2或a=107. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、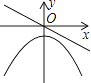 B、
B、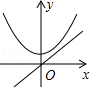 C、
C、 D、
D、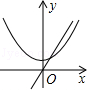 8. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致为( )
8. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致为( )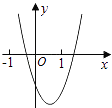 A、
A、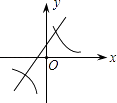 B、
B、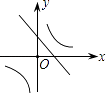 C、
C、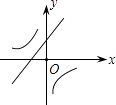 D、
D、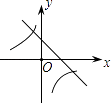 9. 某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是91.设每个枝干长出x个小分支,则x满足的关系式为( )A、x+x2=91 B、1+x2=91 C、1+x+x2=91 D、1+x(x﹣1)=9110. 抛物线y=x2先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A、y=(x+1)2+3 B、y=(x+1)2-3 C、y=(x-1)2-3 D、y=(x-1)2+3
9. 某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是91.设每个枝干长出x个小分支,则x满足的关系式为( )A、x+x2=91 B、1+x2=91 C、1+x+x2=91 D、1+x(x﹣1)=9110. 抛物线y=x2先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A、y=(x+1)2+3 B、y=(x+1)2-3 C、y=(x-1)2-3 D、y=(x-1)2+3二、填空题
-
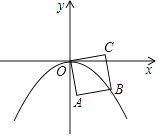
11. 某产品年产量为30台,计划今后每年比前一年的产量增长率为x,试写出两年后的产量y台与x的函数关系式: .12. 如图,是边长为1的正方形OABC绕顶点O顺时针旋转75°后得到的,原正方形的顶点A在x轴的正半轴上,此时点B恰好落在函数y=ax2(a<0)的图象上,则a的值为 .
 13. 已知关于x的函数同时满足下列三个条件:
13. 已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限;
②当想x<2时,对应的函数值y<0;
③当x<2时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是:(写出一个即可)
14. 用一根长为32cm的铁丝围成一个矩形,则围成矩形面积的最大值是 cm2 .15. 当x=m和x=n(m≠n)时,二次函数y=x2﹣2x+3的函数值相等,当x=m+n时,函数y=x2﹣2x+3的值为 .三、解答题
-
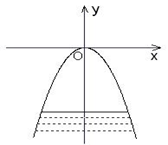
16. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售2件,问他降价多少元时,才能使每天所赚的利润最大?并求出最大利润.17. 拱桥的形状是抛物线,其函数关系式为 , 当水面离桥顶的高度为m时,水面的宽度为多少米?
18. 某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB﹣﹣BC﹣﹣CD所示(不包括端点A).(1)当100<x<200时,直接写y与x之间的函数关系式
(2)蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?
(3)在(2)的条件下,求经销商一次性采购的蔬菜是多少千克时,蔬菜种植基地能获得418元的利润?
 19. 如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
19. 如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
 20. 已知抛物线的C1顶点为E(﹣1,4),与y轴交于C(0,3).
20. 已知抛物线的C1顶点为E(﹣1,4),与y轴交于C(0,3).(1)求抛物线C1的解析式;
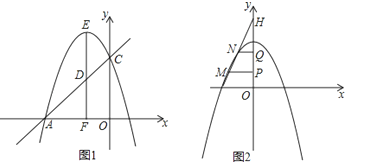
(2)如图1,过顶点E作EF⊥x轴于F点,交直线AC于D,点P、Q分别在抛物线C1和x轴上,若Q为(t,0),且以E、D、P、Q为顶点的四边形为平行四边形,求t的值;
(3)如图2,将抛物线C1向右平移一个单位得到抛物线C2 , 直线y=kx+6与y轴交于点H,与抛物线C2交于M、N两个不同点,分别过M、N两点作y轴的垂线,垂足分别为P、Q,当k的值在取值范围内发生变化时,式子+的值是否发生变化?若不变,请求其值.(解此题时不用相似知识)