江苏省苏州工业园区2015-2016学年七年级上学期数学期末考试试卷

试卷更新日期：2017-12-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列算式中，运算结果为负数的是（）

A、-3² B、|-3| C、－（－3） D、（－3）²

查看试题解析
2. 苏州地铁4号线，2017年上半年通车试运营，主线全程长约为42000m，北起相城区荷塘月色公园，南至吴江同津大道站，共设31站。将42000用科学记数法表示应为（）

A、0.42×10⁵ B、4.2×10⁴ C、44×10³ D、440×10²

查看试题解析
3. 如果 $x > y$ ，则下列变形中正确的是（）

A、 $- \frac{1}{2} x > - \frac{1}{2} y$ B、 $\frac{1}{2} x < \frac{1}{2} y$ C、 $3 x > 5 y$ D、 $x - 3 > y - 3$

查看试题解析
4. 如果 $| x - 2 | = 2 - x$ ，那么 $x$ 的取值范围是（）

A、x≤2； B、x≥2； C、x＜2； D、x＞2；

查看试题解析
5. 已知代数式x+2y的值是3，则代数式2x+4y+1的值是（　　）

A、1 B、4 C、7 D、不能确定

查看试题解析
6. 如图，若 $C$ 为线段 $A B$ 的中点， $D$ 在线段 $C B$ 上， $D A = 6$ ， $D B = 4$ ，则 $C D$ 的长度是（）

A、0.5 B、1 C、1.5 D、2

查看试题解析
7. 若∠A， ∠B互为补角，且∠A﹤∠B，则∠A的余角是（）

A、（∠A+∠B） B、 ∠B C、（∠B－∠A） D、 ∠A

查看试题解析
8. 下边给出的是某月的日历表，任意圈出一竖列上、相邻的三个数，请你运用方程思想来研究，发现这三个数的和不可能（）

A、27 B、40 C、54 D、69

查看试题解析
9. －件工作，甲单独做20 h完成，乙单独做12 h完成，现甲单独做4h后，乙加入和甲一起做，还要几小时完成？若设还要x h完成，则依题意可列方程为（）

A、 $\frac{4}{20} - \frac{x}{20} - \frac{x}{12} = 1$ B、 $\frac{4}{20} - \frac{x}{20} + \frac{x}{12} = 1$ C、 $\frac{4}{20} + \frac{x}{20} - \frac{x}{12} = 1$ D、 $\frac{x}{20} + \frac{4}{20} + \frac{x}{12} = 1$

查看试题解析
10. 钟面角是指时钟的时针与分针所成的角，如果时间从下午2点整到下午4点整，钟面角为90°的情况有（　　）

A、有一种 B、有二种 C、有三种 D、有四种

查看试题解析

二、填空题

11. 单项式 $- \frac{5}{3} a^{2} b c$ 的次数是．

查看试题解析
12. 若单项式2x²y^m与－ $\frac{1}{3}$ xⁿy³是同类项，则m+n的值是

查看试题解析
13. 在数轴上与2的距离等于3个单位的点表示的数是

查看试题解析
14. 不等式 $\frac{1 + x}{2} \geq \frac{2 x - 1}{3}$ 的非负整数解的和是.

查看试题解析
15. 如图，直线AB、CD相交于点O，∠DOE=∠BOD，OF平分∠AOE，若∠BOD=32°，则∠BOF=

查看试题解析
16. 如图，该平面展开图按虚线折叠成正方体后，相对面上两个数之和为8，则x+y＝．

查看试题解析
17. 若有理数a、b、c在数轴上的位置如图所示，则化简：| a |＋| a－b |－| c＋b |＝．

查看试题解析
18. 如图，若开始输入的x的值为正整数，最后输出的结果为144，则满足条件的 $x$ 的值为．

查看试题解析

三、解答题

19. 计算

(1)、

(2)、77°53′26"＋33.3°

查看试题解析
20. 解关于x的方程与不等式

(1)、4-x=3（2-x）

(2)、 $1 - \frac{2 - 3 x}{5} > \frac{1 + x}{2}$ ；

查看试题解析
21. 一个角比它的余角大20°，求这个角的度数．

查看试题解析
22. 用五个小正方体搭成如图的几何体，请画出它的三视图。

查看试题解析
23. 已知不等式 $3 (x - 2) + 10 < 4 (x - 1) + 6$ 的最小整数解为方程 $2 x - y x = 6$ 的解，求代数式 $- 9 y + 6 x^{2} + 3 (y - \frac{2}{3} x^{2})$ 的值.

查看试题解析
24. 如图，一副三角板的两个直角顶点重合在一起．

(1)、若∠EON=140°，求∠MOF的度数；

(2)、比较∠EOM与∠FON的大小，并写出理由；

(3)、求∠EON+∠MOF的度数．

查看试题解析
25. 如图，每个小方格都是边长为1个单位的小正方形，A，B，C三点都是格点（每个小方格的顶点叫格点）．

(1)、找出格点D，画AB的平行线CD；找出格点E，画AB的垂线AE；

(2)、计算格点△ABC的面积．

查看试题解析
26. 我国某部边防军小分队成一列在野外行军，通讯员在队伍中，数了一下他前后的人数，发现前面人数是后面的两倍，他往前超了6位战士，发现前面的人数和后面的人数一样.

(1)、这列队伍一共有多少名战士？

(2)、这列队伍要过一座320米的大桥，为安全起见，相邻两个战士保持相同的一定间距，行军速度为5米/秒，从第一位战士刚上桥到全体通过大桥用了100秒时间，请问相邻两个战士间距离为多少米（不考虑战士身材的大小）？

查看试题解析
27. 如图：已知A、B、C是数轴上的三点，点C表示的数是6，BC=4，AB=12，

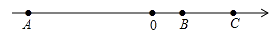(1)、写出数轴上A、B两点表示的数；

(2)、动点P、Q分别从A、C同时出发，点P以每秒2个单位长度的速度沿数轴向右匀速运动，点Q以每秒1个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒，t为何值时，原点O、与P、Q三点中，有一点恰好是另两点所连线段的中点.

查看试题解析