江苏省南京市栖霞等区2015-2016学年七年级上学期数学期末考试试卷
试卷更新日期：2017-12-26 类型：期末考试
一、单选题
-
1. 计算|﹣3|的结果是（ ）A、3 B、- C、﹣3 D、2. 一种面粉的质量标识为“50±0.25千克”，则下列面粉中合格的是（ ）
A、50.30千克 B、49.51千克 C、49.80千克 D、50.70千克3. 下列各题中合并同类项，结果正确的是（ ）A、2a2+3a2=5a2 B、2a2+3a2=6a2 C、4xy﹣3xy=1 D、2x3+3x3=5x64. 下列现象：①用两个钉子就可以把木条固定在墙上．
②从A地到B地架设电线，总是尽可能沿着线段AB架设．
③植树时，只要确定两棵树的位置，就能确定同一行树所在的直线．
④把弯曲的公路改直，就能缩短路程．
其中能用“两点确定一条直线”来解释的现象有（ ）
A、①② B、①③ C、②④ D、③④5. 关于x的方程﹣ax=b（a≠0）的解是（ ）A、x= B、x=﹣ C、x=﹣ D、x=6. 点C在线段AB上，不能判定点C是线段中点的是（ ）
A、AC=BC B、AB=2AC C、AC+BC=AB D、AC= AB7. 观察下图，请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来（ ）
A、
B、
C、
D、
8. 数轴上三个点表示的数分别为p、r、s．若p﹣r=5，s﹣p=2，则s﹣r等于（ ）A、3 B、﹣3 C、7 D、﹣7二、填空题
-
9. ﹣ 的倒数是 ， 相反数是 ．10. 六棱柱有 面．11. 马拉松（Marathon）国际上非常普及的长跑比赛项目，全程距离26英里385码，折合为42195米，用科学记数法表示42195为 ．12. 已知∠α=34°，则∠α的补角为°．13. 请列举一个单项式，使它满足系数为2，次数为3，含有字母a、b，单项式可以为 ．14. 已知x＜﹣1，则x、x2、x3的大小关系是 ．15. 如图，将一副三角板的直角顶点重合，摆放在桌面上，若∠BOC=63°，则∠AOD= ．
16. 某商店在进价的基础上提高50元作零售价销售，商店又以8折（即售价的80%）的价格开展促销活动，这时一件商品所获利润为20元，则该商品进价为元．17. 如图，下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么黄色的对面是 ．
18. 计算（ ）﹣2×（ ）﹣3×（ ﹣ ）的结果是 ．三、解答题
-
19. 计算：
(1)、﹣11﹣（﹣3）×6；(2)、[（﹣2）2﹣3 2]÷ ．20. 先化简，再求值：2（x2﹣xy）﹣（3x2﹣6xy），其中x= ，y=﹣1．21. 解方程：(1)、4（x﹣1）﹣3（2x+1）=7；(2)、 ．22. 如图，已知AB=7，BC=3，点D为线段AC的中点，求线段DB的长度．
23. 如图是由一些棱长都为1cm的小正方体组合成的简单几何体．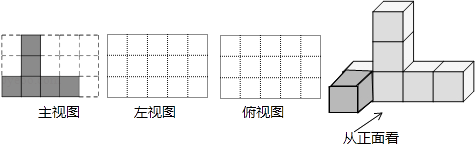
(1)、该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；
(2)、如果在这个几何体上再添加一些小正方体，并保持俯视图和左视图不变，最多可以再添加块小正方体．
24. 把一些图书分给某班学生阅读，如果每人分3本则剩余20本；如果每人分4本，则还缺25本．这个班有多少学生？25. 扬子江药业集团生产的某种药品的长方体包装盒的侧面展开图如图所示．根据图中数据，如果长方体盒子的长比宽多4cm，求这种药品包装盒的体积．
26. 几何知识可以解决生活中许多距离最短的问题．让我们从书本一道习题入手进行知识探索．(1)、【回忆】如图，A、B是河l两侧的两个村庄．现要在河l上修建一个抽水站C，使它到A、B两村庄的距离的和最小，请在图中画出点C的位置，并说明理由．
(2)、【探索】如图，A、B两个村庄在一条笔直的马路的两端，村庄 C在马路外，要在马路上建一个垃圾站O，使得AO+BO+CO最小，请在图中画出点O的位置，并说明理由．
(3)、如图，A、B、C、D四个村庄，现建一个垃圾站O，使得AO+BO+CO+DO最小，请在图中画出点O的位置，并说明理由．
27. 综合题(1)、如图1，若CO⊥AB，垂足为O，OE、OF分别平分∠AOC与∠BOC．求∠EOF的度数；
(2)、如图2，若∠AOC=∠BOD=80°，OE、OF分别平分∠AOD与∠BOC．求∠EOF的度数；
(3)、若∠AOC=∠BOD=α，将∠BOD绕点O旋转，使得射线OC与射线OD的夹角为β，OE、OF分别平分∠AOD与∠BOC．若α+β≤180°，α＞β，则∠EOC= ． （用含α与β的代数式表示）