江苏省无锡市惠山区2016届九年级上学期数学期末考试试卷
试卷更新日期:2017-12-26 类型:期末考试
一、单选题
-
1. 若 ,则 的值为( )A、 B、 C、1 D、
-
2. 下列方程有实数根的是( )
A、x2+10=0 B、x2+x+1=0 C、x2﹣x﹣1=0 D、x2﹣ x+1=0 -
3. 已知:在Rt△ABC中,∠C=90°,sinA= , 则cosB的值为( )A、 B、 C、 D、
-
4. 小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )A、255分 B、84分 C、84.5分 D、86分
-
5. 某圆锥的母线长为6cm,其底面圆半径为3cm,则它的侧面积为( )A、18πcm2 B、18cm2 C、36πcm2 D、36cm2
-
6. 已知:⊙O是△ABC的外接圆,∠OAB=40°,则∠ACB的大小为( )A、20° B、50° C、20°或160° D、50°或130°
-
7. 将一副三角板按图叠放,则△AOB与△COD的面积之比为( )
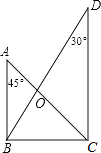 A、1: B、1:3 C、1: D、1:2
A、1: B、1:3 C、1: D、1:2 -
8. 如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的各顶点称为格点,直角△ABC的顶点均在格点上,则满足条件的点C有( )
 A、6个 B、8个 C、10个 D、12个
A、6个 B、8个 C、10个 D、12个 -
9. 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
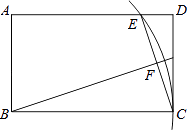 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2﹣kx<0的解集为( )
 A、0<x<1 B、﹣1<x<0 C、x<0或x>1 D、x<﹣1或x>0
A、0<x<1 B、﹣1<x<0 C、x<0或x>1 D、x<﹣1或x>0
二、填空题
-
11. 方程2x2+4x﹣1=0的两根为x1 , x2 , 则x1+x2= .
-
12. 若△ABC∽△ACD,AB=1,AD=4,则AC=
-
13. 在等腰Rt△ABC中,AB=AC,则tanB= .
-
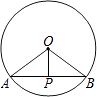
14. 如图,AB为⊙O的弦,AB=8,OA=5,OP⊥AB于P,则OP= .
-
15. 将二次函数y=x2﹣2x+3的图象先向上平移2个单位,再向右平移3个单位后,所得新抛物线的顶点坐标为 .
-
16. 已知二次函数y=﹣x2+bx+c,当2<x<5时,y随x的增大而减小,则实数b的取值范围是 .
-
17. 如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长 .

-
18. 已知:等边△ABC的边长为2,点D为平面内一点,且BD= AD=2 ,则CD= .
三、解答题
-
19. 计算:(1)、(﹣ )2+|﹣2|﹣(﹣2)0;(2)、(x+2)2﹣2(x+2).
-
20. 计算题
(1)、解不等式:3(x+2)<5x;
(2)、解方程:x2﹣2x﹣1=0. -
21. 甲、乙两支仪仗队各10名队员的身高(单位:cm)如下表:
甲队
179
177
178
177
178
178
179
179
177
178
乙队
178
178
176
180
180
178
176
179
177
178
(1)、甲队队员的平均身高为cm,乙队队员的平均身高为cm;(2)、请用你学过的统计知识判断哪支仪仗队的身高更为整齐呢? -
22. 在一个不透明的口袋中,放有三个标号分别为1,2,3的质地、大小都相同的小球.任意摸出一个小球,记为x,再从剩余的球中任意摸出一个小球,又记为y,得到点(x,y).
(1)、用画树状图或列表等方法求出点(x,y)的所有可能情况;(2)、求点(x,y)在二次函数y=ax2﹣4ax+c(a≠0)图象的对称轴上的概率. -
23. 已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.
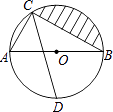 (1)、求BC及阴影部分的面积;(2)、求CD的长.
(1)、求BC及阴影部分的面积;(2)、求CD的长. -
24. 如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?
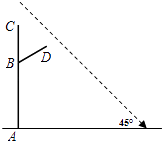
-
25. 某公司销售一种进价为20 (元/个)的计算器,其销售量y (万个)与销售价格x (元/个)之间为一次函数关系,其变化如下表:
价格x (元/个)
…
30
50
…
销售量y (万个)
…
5
3
…
同时,销售过程中的其他开支(不含进价)总计40万元.若该公司要获得40万元的净利润,且尽可能让顾客得到实惠,那么销售价格应定为多少?
(注:净利润=总销售额﹣总进价﹣其他开支)
-
26. 如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
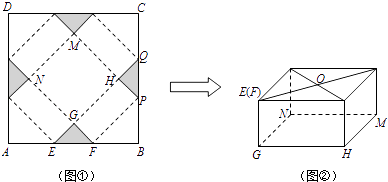 (1)、求线段GF的长;(用含x的代数式表示)(2)、当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?(3)、试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
(1)、求线段GF的长;(用含x的代数式表示)(2)、当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?(3)、试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由. -
27. 如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB= .
 (1)、若点Q是线段BC上一点,且点Q的横坐标为m.
(1)、若点Q是线段BC上一点,且点Q的横坐标为m.①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)、若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
-
28. 如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
 (1)、求∠ABC的度数;(2)、若点D是第四象限内抛物线上一点,△ADC的面积为 ,求点D的坐标;(3)、若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
(1)、求∠ABC的度数;(2)、若点D是第四象限内抛物线上一点,△ADC的面积为 ,求点D的坐标;(3)、若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
