江苏省泰州市姜堰区2016届九年级上学期数学期末考试试卷
试卷更新日期：2017-12-26 类型：期末考试
一、单选题
-
1. 已知x=2是一元二次方程x2﹣mx﹣6=0的一个解，则m的值为（ ）
A、﹣1 B、1 C、﹣3 D、2或﹣32. 如果∠α是等边三角形的一个内角，那么cosα的值等于（ ）A、 B、 C、 D、13. 书架上有数学书2本，英语书3本，语文书5本，从中任意抽取一本是数学书的概率是（ ）
A、 B、 C、 D、4. 如图，A、B、C是⊙O上的三个点，∠ABC=25°，则∠AOC的度数是 （ ）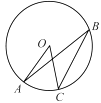
A、25° B、65° C、50° D、130°5. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9环，方差依次为0.56、0.65、0.51、0.40，则成绩最稳定的是（ ）
A、甲 B、乙 C、丙 D、丁6. 已知二次函数y=a（x﹣h）2+k（a，h，k为常数）在坐标平面上的图象通过（0，5）、（15，8）两点．若a＜0，0＜h＜10，则h之值可能为下列何值？（ ）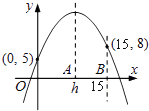
A、5 B、6 C、7 D、8二、填空题
-
7. 若△ABC∽△DEF，且△ABC与△DEF的相似比为1：2，则△ABC与△DEF的面积比为 ．
8. 圆内接四边形ABCD中，∠A：∠C=1：5，则∠C的度数为度．
9. 已知x（x﹣3）=5，则代数式2x2﹣6x﹣5的值为 ．
10. 学校篮球集训队11名队员进行定点投篮训练，11名队员在1分钟内投进篮框的球数和人数如下表：球数/个
6
7
8
9
10
12
人数
1
1
1
4
3
1
则11名队员投进篮框的球数的中位数是 个．
11. 飞机着陆后滑行的距离S（单位：m）与滑行的时间t（单位：s）的函数关系式是S=80t﹣2t2 ， 飞机着陆后滑行的最远距离是m．
12. 如图，已知▱ABCD，∠A=45°，AD=4，以AD为直径的半圆O与BC相切于点B，则图中阴影部分的面积为（结果保留π）．
13. 根据图中所标注的数据，计算此圆锥的侧面积cm2（结果保留π）．
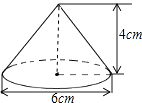14. 如图，一束光线照在坡度为1： 的斜坡上，被斜坡上的平面镜反射成与地面平行的光线，则这束光线与坡面的夹角α是度．
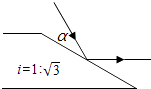15. ⊙O的半径为5，弦BC=8，点A是⊙O上一点，且AB=AC，直线AO与BC交于点D，则AD的长为 ．
16. 若二次函数y=（k﹣2）x2+（2k+1）x+k的图象与x轴有两个交点，其中只有一个交点落在﹣1和0之间（不包括﹣1和0），那么k的取值范围是 ．
三、解答题
-
17. 计算题(1)、计算：（3﹣π）0+（﹣ ）﹣2+ ﹣2|sin45°﹣1|；(2)、先化简，再求值： ，其中实数m使关于x的一元二次方程x2﹣4x﹣m=0有两个相等的实数根．18. 雾霾天气严重影响市民的生活质量．在去年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．
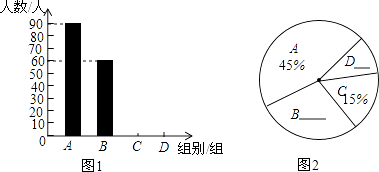
组别
雾霾天气的主要成因
百分比
A
工业污染
45%
B
汽车尾气排放
m
C
炉烟气排放
15%
D
其他（滥砍滥伐等）
n
(1)、本次被调查的市民共有多少人？(2)、求m、n的值，并计算图2中区域B所对应的扇形圆心角的度数；
(3)、若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？
19. 已知关于x的一元二次方程（m+1）x2﹣（m+3）x+2=0．
(1)、证明：不论m为何值时，方程总有实数根；(2)、m为何整数时，方程有两个不相等的正整数根．
20. 从A、B、C、D四人中随机选择两人参加乒乓球比赛，请用树状图或列表法求下列事件发生的概率．(1)、A参加比赛；
(2)、A、B都参加比赛．
21. 如图，在△ABC中，∠ABC=90°，BC=6，D为AC延长线上一点，AC=3CD，过点D作DH∥AB，交BC的延长线于点H．
(1)、求BH的长；(2)、若AB=12，试判断∠CBD与∠A的数量关系，请说明理由．
22. 如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走9m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．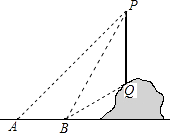
(1)、求∠BPQ的度数；(2)、求该电线杆PQ的高度．（结果保留根号）23. 某工厂为了对新研发的一种产品进行合理定价，将该产品按拟定的价格进行试销，通过对5天的试销情况进行统计，得到如下数据：单价（元/件）
25
28
35
40
42
销量（件）
50
44
30
20
16
(1)、通过对上面表格中的数据进行分析，发现销量y（件）与单价x（元/件）之间存在一次函数关系，求y关于x的函数关系式（不需要写出函数自变量的取值范围）；(2)、预计在今后的销售中，销量与单价仍然存在（1）中的关系，且该产品的成本是20元/件．为使工厂获得最大利润，该产品的单价应定为多少？
24. 如图，PQ为圆O的直径，点B在线段PQ的延长线上，OQ=QB=1，动点A在圆O的上半圆运动（含P、Q两点），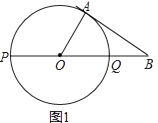
(1)、当线段AB所在的直线与圆O相切时，求弧AQ的长（图1）；
(2)、若∠AOB=120°，求AB的长（图2）；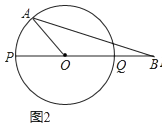
(3)、如果线段AB与圆O有两个公共点A、M，当AO⊥PM于点N时，求tan∠MPQ的值（图3）．
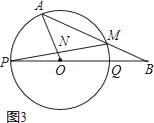25. 如图，在平面直角坐标系中，▱ABCD的顶点的坐标分别为A（﹣6，9），B（0，9），C（3，0），D（﹣3，0），抛物线y=ax2+bx+c（a，b，c为常数，且a≠0）过A、B两点，顶点为M．
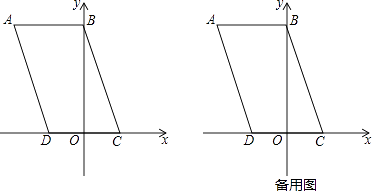(1)、若抛物线过点C，求抛物线的解析式；(2)、若抛物线的顶点M落在△ACD的内部（包括边界），求a的取值范围；(3)、若a＜0，连结CM交线段AB于点Q（Q不与点B重合），连接DM交线段AB于点P，设S1=S△ADP+S△CBQ ， S2=S△MPQ ， 试判断S1与S2的大小关系，并说明理由．