江苏省苏州市高新区2016届九年级上学期数学期末考试试卷

试卷更新日期：2017-12-26 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²-2x=0的根是（）

A、 $x = 2$ B、 $x = 0$ C、 $x_{1} = - 2$ ， $x_{2} = 0$ D、 $x_{1} = 2$ ， $x_{2} = 0$

查看试题解析
2. 在平面直角坐标系中，将二次函数y=2x²的图象向上平移2个单位，所得函数图象的解析式为（）

A、 $y = 2 x^{2} + 2$ B、 $y = 2 x^{2} - 2$ C、 $y = 2 {(x - 2)}^{2}$ D、 $y = 2 {(x + 2)}^{2}$

查看试题解析
3. 有一组数据：3，5，5，6，7．这组数据的众数为（）

A、3 B、5 C、6 D、7

查看试题解析
4. 下列命题：
①长度相等的弧是等弧；
②任意三点确定一个圆；
③相等的圆心角所对的弦相等；
④外心在三角形的一条边上的三角形是直角三角形．
其中，真命题有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 如图，已知⊙O的两条弦AC，BD相交于点E，∠A=70^o ， ∠C=50^o ，那么sin∠AEB的值为（）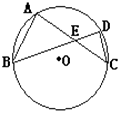

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 下列四个函数图象中，当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大的是（）

A、 B、 C、 D、

查看试题解析
7. 已知直角三角形 $A B C$ 中，斜边 $A B$ 的长为 $m$ ， $∠ B = 40^{\circ}$ ，则直角边 $B C$ 的长是（）

A、 $m \sin 40^{\circ}$ B、 $m \tan 40^{\circ}$ C、 $m \cos 40^{\circ}$ D、 $\frac{m}{\tan 40^{\circ}}$

查看试题解析
8. 如右图是一个正八边形，图中空白部分的面积等于20，则阴影部分的面积等于（）

A、20 B、 $10 \sqrt{2}$ C、18 D、 $20 \sqrt{2}$

查看试题解析
9. 二次函数 $y = a x^{2} + b x + c$ （a，b，c为常数，且 $a \neq 0$ ）中的 $x$ 与 $y$ 的部分对应值如表：
$x$
…
－1
0
1
3
…
$y$
…
－1
3
5
3
…
下列结论：
① $a c < 0$ ；
②当 $x > 1$ 时，y的值随x值的增大而减小；
③3是方程 $a x^{2} + (b - 1) x + c = 0$ 的一个根；
④当 $- 1 < x < 3$ 时， $a x^{2} + (b - 1) x + c > 0$ ．
其中正确的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 如图，在扇形铁皮AOB中，OA=20，∠AOB=36°，OB在直线 $l$ 上．将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA第一次落在l上时，停止旋转．则点O所经过的路线长为
（）

A、 $20 π$ B、 $22 π$ C、 $24 π$ D、 $20 π + 10 \sqrt{5} - 10$

查看试题解析

二、填空题

11. 数据3、1、0、－1、－3的方差是．

查看试题解析
12. 袋中有4个红球，x个黄球，从中任摸一个恰为黄球的概率为 $\frac{3}{4}$ ，则x的值为．

查看试题解析
13. 如图，AB是⊙O的直径，AC是弦，若∠ACO=32°，则∠COB的度数等于．

查看试题解析
14. 一圆锥的侧面积为 $15 π$ ，底面半径为3，则该圆锥的母线长为．

查看试题解析
15. 已知抛物线 $y = a x^{2} + b x + c$ （ $a$ <0）过A（ $- 2$ ，0）、O（0，0）、B（ $- 3$ ， $y_{1}$ ）、C（3， $y_{2}$ ）四点．则 $y_{1}$ $y_{2}$ （用“＜”，“＞”或“=”填空）．

查看试题解析
16. 如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆与BC相切于点D，分别交AC、AB于点E、F．若AC=6，AB=10，则⊙O的半径为．

查看试题解析
17. 如图，已知A、B两点的坐标分别为（－4，0）、（0，2），⊙C的圆心坐标为（0，－2），半径为2．若D是⊙C上的一个动点，射线AD与 $y$ 轴交于点E，则△ABE面积的最大值是．

查看试题解析
18. 如图，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴的一个交点A在点（－2，0）和（1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则 $a$ 的取值范围是．

查看试题解析

三、解答题

19. 计算题

(1)、计算： $2 \sin 30 ° - {(2015 - π)}^{0} + | 1 - \tan 60 ° |$ ；

(2)、解方程： ${(x - 2)}^{2} = 3 (x - 2)$ ．

查看试题解析
20. 已知关于x的一元二次方程x²-2（m-1）x-m（m+2）=0．

(1)、求证：方程总有两个不相等的实数根；

(2)、若x=-2是此方程的一个根，求代数式2018-3（m-1）²的值．

查看试题解析
21. 如图，点A、B、C是⊙O上的三点，AB∥OC．

(1)、求证：AC平分∠OAB；

(2)、过点O作OE⊥AB于点E，交AC于点P．若AB=2，∠AOE=30°，求PE的长．

查看试题解析
22. 如图二次函数的图象经过A（－1，0）和B（3，0）两点，且交 $y$ 轴于点C．

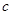(1)、试确定、的值；

(2)、若点M为此抛物线的顶点，求△MBC的面积．

查看试题解析
23. 李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩．她从中随机调查了若干名女生的测试成绩（单位：米），并将统计结果绘制成了如下的统计图表（内容不完整）．
测试成绩
$3 \leq x < 4$
$4 \leq x < 5$
$5 \leq x < 6$
$6 \leq x < 7$
$7 \leq x < 8$
合计
频数
3
27
9
m
1
n

请你结合图表中所提供的信息，回答下列问题：

(1)、表中m= ， n=；

(2)、请补全频数分布直方图；

(3)、在扇形统计图中， $6 \leq x < 7$ 这一组所占圆心角的度数为度；

(4)、如果掷实心球的成绩达到6米或6米以上为优秀，请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数．

查看试题解析
24. 某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费．某顾客刚好消费200元．

(1)、该顾客至少可得到元购物券；

(2)、请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．

查看试题解析
25. 如图，小丽假期在娱乐场游玩时，想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度．她先在山脚下的点E处测得山顶A的仰角是30°，然后，她沿着坡度i=1∶1的斜坡步行15分钟到达C处，此时，测得点A的俯角是15°．已知小丽的步行速度是18米/分，图中点A、B、E、D、C在同一平面内，且点D、E、B在同一水平直线上，求出娱乐场地所在山坡AE的高度AB．（精确到0.1米，参考数据： ≈1.41）．

查看试题解析
26. 某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．

(1)、写出商场销售这种文具，每天所得的销售利润 $w$ （元）与销售单价 $x$ （元）之间的函数关系式；

(2)、求销售单价为多少元时，该文具每天的销售利润最大；（3）商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元．
请比较哪种方案的最大利润更高，并说明理由．

查看试题解析
27. 如图，在平面直角坐标系中，直线 $y = - \frac{4}{3} x + 4$ 分别交x轴、y轴于A、B两点．

(1)、求A、B两点的坐标；

(2)、设P是直线AB上一动点（点P与点A不重合），⊙P始终和x轴相切，和直线AB相交于C、D两点（点C的横坐标小于点D的横坐标）．若P点的横坐标为m，试用含有m的代数式表示点C的横坐标；

(3)、在（2）的条件下，若点C在线段AB上，当△BOC为等腰三角形时求m的值．

查看试题解析
28. 如图，在平面直角坐标系中，直线 $y = \frac{3}{4} x - \frac{3}{2}$ 与抛物线 $y = - \frac{1}{4} x^{2} + b x + c$ 交于A、B两点，点A在x轴上，点B的横坐标为－8．

(1)、求该抛物线的解析式；

(2)、点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．
①设△PDE的周长为 $l$ ，点P的横坐标为 $x$ ，求 $l$ 关于 $x$ 的函数关系式，并求出 $l$ 的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在 $y$ 轴上时，求出对应点P的坐标．

查看试题解析

测试成绩	$3 \leq x < 4$	$4 \leq x < 5$	$5 \leq x < 6$	$6 \leq x < 7$	$7 \leq x < 8$	合计
频数	3	27	9	m	1	n

$x$	…	－1	0	1	3	…
$y$	…	－1	3	5	3	…