江苏省南通市海门市2016届九年级上学期数学期末考试试卷

试卷更新日期：2017-12-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，为无理数的是（）

A、0.2 B、 $\frac{1}{2}$ C、 $\sqrt{2}$ D、﹣5

查看试题解析
2. 下列算式中，正确的是（）

A、3a²﹣4a²=﹣1 B、（a³b）²=a³b² C、（﹣a²）³=a⁶ D、a²÷a=a

查看试题解析
3. 一个几何体的主视图和左视图都是矩形，俯视图是圆，则这个几何体是（）

A、三棱柱 B、圆柱 C、三棱锥 D、圆锥

查看试题解析
4. 数据：2，5，4，5，3，4，4的众数与中位数分别是（）

A、4，3 B、4，4 C、3，4 D、4，5

查看试题解析
5. 在函数y= $\sqrt{x - 1}$ 中，自变量x的取值范围是（）

A、x≤1 B、x≥1 C、x＜1 D、x＞1

查看试题解析
6. 在不透明的布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，则摸出红球的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2），以原点O为位似中心，相似比为 $\frac{1}{2}$ ，把△EFO缩小，则点E的对应点E′的坐标是（）

A、（﹣2，1） B、（﹣8，4） C、（﹣8，4）或（8，﹣4） D、（﹣2，1）或（2，﹣1）

查看试题解析
8. 如图，AB是⊙O的直径，TA切⊙O于点A，连结TB交⊙O于点C，∠BTA=40°，点M是圆上异于B，C的一个动点，则∠BMC的度数等于（）

A、50° B、50°或130° C、40° D、40°或140°

查看试题解析
9. 如图反映的过程是小明从家去食堂吃早餐，接着去图书馆读报，然后回家．其中x表示时间，y表示小明离家的距离，小明家、食堂、图书馆在同一直线上．根据图中提供的信息，有下列说法：
①食堂离小明家0.4km；
②小明从食堂到图书馆用了3min；
③图书馆在小明家和食堂之间；
④小明从图书馆回家的平均速度是0.04km/min．
其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 如图，四边形ABCD为正方形，边长为4，点F在AB边上，E为射线AD上一点，正方形ABCD沿直线EF折叠，点A落在G处，已知点G恰好在以AB为直径的圆上，则CG的最小值等于（）

A、0 B、2 $\sqrt{5}$ C、4﹣2 $\sqrt{5}$ D、2 $\sqrt{5}$ ﹣2

查看试题解析

二、填空题

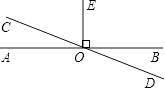
11. 反比例函数 $y = \frac{1}{x}$ 的图象在象限．

查看试题解析
12. 分解因式：（a+b）²﹣4ab= ．

查看试题解析
13. 如图，直线AB，CD相交于点O，OE⊥AB，∠BOD=20°，则∠COE等于度．

查看试题解析
14. 如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有对全等三角形．

查看试题解析
15. 一个圆锥的侧面积为12πcm² ，母线长为6cm，则这个圆锥底面圆的半径为cm．

查看试题解析
16. 在平面直角坐标系中，将抛物线y=x²﹣4先向右平移2个单位，再向上平移2个单位，得到的抛物线解析式为．

查看试题解析
17. 如图，将△ABC绕点B逆时针旋转40°，得到△A′B′C′，若点C′恰好落在边BA的延长线上，且A′C′∥BC，连接CC′，则∠ACC′=度．

查看试题解析
18. 已知关于x的方程x²+2（a﹣1）x+a²﹣7a﹣4=0的两根为x₁ ， x₂ ，且满足（2x₁﹣3）（2x₂﹣3）=29，则a的值为．

查看试题解析

三、解答题

19. 计算题

(1)、计算： $\sqrt{12}$ ﹣2^﹣1+| $\sqrt{3}$ ﹣2|﹣3sin30°

(2)、先化简，再求值： $\frac{a - 2}{a^{2} - 1}$ ÷（ $\frac{1}{a - 1}$ ﹣1），其中a=3．

查看试题解析
20. 解不等式组 ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 2 < 3 (x + 2) \end{array}$ ，并求出所有正整数解的和．

查看试题解析
21. 已知：菱形OBCD在平面直角坐标系中位置如图所示，点B的坐标为（2，0），∠DOB=60°．

(1)、点D的坐标为，点C的坐标为；

(2)、若点P是对角线OC上一动点，点E（0，﹣ $\sqrt{3}$ ），求PE+PB的最小值．

查看试题解析
22. 小明同学在用描点法画二次函数y=ax²+bx+c图象时，由于粗心，他算错了一个y值，列出了下面表格：
　x
…
﹣1　
0
1　
2
3　
…
　y=ax²+bx+c
…
5
3　
2
3
6
…

(1)、请指出这个错误的y值，并说明理由；

(2)、若点M（a，y₁），N（a+4，y₂）在二次函数y=ax²+bx+c图象上，且a＞﹣1，试比较y₁与y₂的大小．

查看试题解析
23. 如图，一枚棋子放在⊙O上的点A处，通过摸球来确定该棋子的走法．
其规则如下：在一只不透明的口袋中，装有3个标号分别为1，2，3的相同小球．充分搅匀后从中随机摸出1个，记下标号后放回袋中并搅匀，再从中随机摸出1个，若摸出的两个小球标号之积是m，就沿着圆周按逆时针方向走m步（例如：m=1，则A﹣B；若m=6，则A﹣B﹣C﹣D﹣A﹣B﹣C）．用列表或树状图，分别求出棋子走到A、B、C、D点的概率．

查看试题解析
24. “科学”号是我国目前最先进的海洋科学综合考察船，它在南海利用探测仪在海面下方探测到点C处有古代沉船．如图，海面上两探测点A，B相距1400米，探测线与海面的夹角分别是30°和60°．试确定古代沉船所在点C的深度．（结果精确到1米，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
25. 如图，在⊙O中，OE垂直于弦AB，垂足为点D，交⊙O于点C，∠EAC=∠CAB．

(1)、求证：直线AE是⊙O的切线；

(2)、若AB=8，sin∠E= $\frac{3}{5}$ ，求⊙O的半径．

查看试题解析
26. 码头工人每天往一艘轮船50吨货物，装载完毕恰好用了8天时间．

(1)、轮船到达目的地后开始卸货，平均卸货速度v（单位：吨/天）与卸货时间t（单位：天）之间有怎样的函数关系？

(2)、由于遇到紧急情况，要求船上的货物不超过5天卸货完毕，那么平均每天至少要卸多少吨货物？

(3)、若原有码头工人10名，在（2）的条件下，至少需要增加多少名工人才能完成任务？

查看试题解析
27. 如图，已知在矩形ABCD中，BC=2CD=2a，点E在边CD上，在矩形ABCD的左侧作矩形ECGF，使CG=2GF=2b，连接BD，CF，连结AF交BD于点H．

(1)、求证：BD∥CF；

(2)、求证：H是AF的中点；

(3)、连结CH，若HC⊥BD，求a：b的值．

查看试题解析
28. 如图，双曲线y= $\frac{k}{x}$ 经过点A（1，2），过点A作y轴的垂线，垂足为B，交双曲线y=﹣ $\frac{18}{x}$ 于点C，直线y=m（m≠0）分别交双曲线y=﹣ $\frac{18}{x}$ 、y= $\frac{k}{x}$ 于点P、Q．

(1)、求k的值；

(2)、若△OAP为直角三角形，求点P的坐标；

(3)、△OCQ的面积记为S_△_OCQ ， △OAP的面积记为S△OAP，试比较S_△_OCQ与S_△_OAP的大小（直接写出结论）．

查看试题解析

x	…	﹣1	0	1	2	3	…
y=ax²+bx+c	…	5	3	2	3	6	…