江苏省南京市玄武区2016届九年级上学期数学期末考试试卷

试卷更新日期：2017-12-26 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²=1的解是（　　）

A、x=1 B、x=﹣1 C、x=±1 D、x=0

查看试题解析
2. ⊙O的半径为1，同一平面内，若点P与圆心O的距离为1，则点P与⊙O的位置关系是（）

A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法确定

查看试题解析
3. 有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这9名同学成绩的（）

A、众数 B、中位数 C、平均数 D、极差

查看试题解析
4. 已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表，则方程ax²+bx+c=0的一个解的范围是（）
x
6.17
6.18
6.19
6.20
y
﹣0.03
﹣0.01
0.02
0.04

A、﹣0.01＜x＜0.02 B、6.17＜x＜6.18 C、6.18＜x＜6.19 D、6.19＜x＜6.20

查看试题解析
5. 若点A（﹣1，a），B（2，b），C（3，c）在抛物线y=x²上，则下列结论正确的是（）

A、a＜c＜b B、b＜a＜c C、c＜b＜a D、a＜b＜c

查看试题解析
6. 如图，点E在y轴上，⊙E与x轴交于点A，B，与y轴交于点C，D，若C（0，9），D（0，﹣1），则线段AB的长度为（）

A、3 B、4 C、6 D、8

查看试题解析

二、填空题

7. 若 $\frac{b}{a}$ =3，则 $\frac{b + a}{a}$ = ．

查看试题解析
8. 一组数据：2，3，﹣1，5的极差为．

查看试题解析
9. 一元二次方程x²﹣4x+1=0的两根是x₁ ， x₂ ，则x₁•x₂的值是．

查看试题解析
10. 制造一种产品，原来每件的成本是100元，由于连续两次降低成本，现在的成本是81元，则平均每次降低成本的百分率为

查看试题解析
11. 在平面直角坐标系中，将抛物线y=2x²先向右平移3个单位，再向上平移1个单位，得到的抛物线的函数表达式为．

查看试题解析
12. 已知圆锥的底面半径为6cm，母线长为8cm，它的侧面积为cm² ．

查看试题解析
13. 如图，根据所给信息，可知 $\frac{B C}{B^{'} C^{'}}$ 的值为．

查看试题解析
14. 已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表，则当x=3时，y= ．
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
7
3
1
1
3
…

查看试题解析
15. 如图，AB是⊙O的一条弦，C是⊙O上一动点且∠ACB=45°，E、F分别是AC、BC的中点，直线EF与⊙O交于点G、H．若⊙O的半径为2，则GE+FH的最大值为．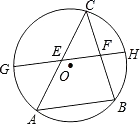

查看试题解析
16. 如图，在矩形ABCD中，M、N分别是边AD、BC的中点，点P、Q在DC边上，且PQ= $\frac{1}{4}$ DC．若AB=16，BC=20，则图中阴影部分的面积是．

查看试题解析

三、解答题

17. 计算题

(1)、解方程：（x+1）²=9；

(2)、解方程：x²﹣4x+2=0．

查看试题解析
18. 已知关于x的一元二次方程（a+1）x²﹣x+a²﹣2a﹣2=0有一根是1，求a的值．

查看试题解析
19. 射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5

(1)、完成表中填空①；②；

(2)、请计算甲六次测试成绩的方差；

(3)、若乙六次测试成绩方差为 $\frac{4}{3}$ ，你认为推荐谁参加比赛更合适，请说明理由．

查看试题解析
20. 一只不透明的袋子中，装有三个分别标记为“1”、“2”、“3”的球，这三个球除了标记不同外，其余均相同．搅匀后，从中摸出一个球，记录球上的标记后放回袋中并搅匀，再从中摸出一个球，再次记录球上的标记．

(1)、请列出上述实验中所记录球上标记的所有可能的结果；

(2)、求两次记录球上标记均为“1”的概率．

查看试题解析
21. 如图，在半径为2的⊙O中，弦AB长为2．

(1)、求点O到AB的距离．

(2)、若点C为⊙O上一点（不与点A，B重合），求∠BCA的度数．

查看试题解析
22. 已知二次函数y=x²﹣2x﹣3．

(1)、该二次函数图象的对称轴为；

(2)、判断该函数与x轴交点的个数，并说明理由；

(3)、下列说法正确的是（填写所有正确说法的序号）
①顶点坐标为（1，﹣4）；
②当y＞0时，﹣1＜x＜3；
③在同一平面直角坐标系内，该函数图象与函数y=﹣x²+2x+3的图象关于x轴对称．

查看试题解析
23. 如图，在四边形ABCD中，AC、BD相交于点F，点E在BD上，且 $\frac{A B}{A E} = \frac{B C}{E D} = \frac{A C}{A D}$ ．

(1)、求证：∠BAE=∠CAD；

(2)、求证：△ABE∽△ACD．

查看试题解析
24. 课本1.4有这样一道例题：
问题4：用一根长22cm的铁丝：

(1)、能否围成面积是30cm²的矩形？

(2)、能否围成面积是32cm²的矩形？
据此，一位同学提出问题：“用这根长22cm的铁丝能否围成面积最大的矩形？若能围成，求出面积最大值；若不能围成，请说明理由．”请你完成该同学提出的问题．

查看试题解析
25. 如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．

(1)、判断直线AC与⊙O的位置关系，并说明理由；

(2)、当BD=6，AB=10时，求⊙O的半径．

查看试题解析
26. 已知一次函数y=x+4的图象与二次函数y=ax（x﹣2）的图象相交于A（﹣1，b）和B，点P是线段AB上的动点（不与A、B重合），过点P作PC⊥x轴，与二次函数y=ax（x﹣2）的图象交于点C．

(1)、求a、b的值

(2)、求线段PC长的最大值；

(3)、若△PAC为直角三角形，请直接写出点P的坐标．

查看试题解析
27. 如图，折叠边长为a的正方形ABCD，使点C落在边AB上的点M处（不与点A，B重合），点D落在点N处，折痕EF分别与边BC、AD交于点E、F，MN与边AD交于点G．证明：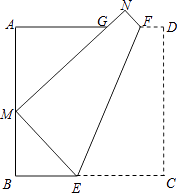

(1)、△AGM∽△BME；

(2)、若M为AB中点，则 $\frac{A M}{3} = \frac{A G}{4} = \frac{M G}{5}$ ；

(3)、△AGM的周长为2a．

查看试题解析

	第一次	第二次	第三次	第四次	第五次	第六次	平均成绩	中位数
甲	10	8	9	8	10	9	9	①
乙	10	7	10	10	9	8	②	9.5

x	6.17	6.18	6.19	6.20
y	﹣0.03	﹣0.01	0.02	0.04

x	…	﹣3	﹣2	﹣1	0	1	…
y	…	7	3	1	1	3	…