江苏省连云港市东海县2016届九年级上学期数学期末考试试卷
试卷更新日期：2017-12-26 类型：期末考试
一、单选题
-
1. 方程x2﹣9=0的解是（ ）A、x=3 B、x=9 C、x=±3 D、x=±92. 在端午节到来之前，学校食堂推荐了A，B，C三家粽子专卖店，对全校师生爱吃哪家店的粽子作调查，以决定最终向哪家店采购，下面的统计量中最值得关注的是（ ）A、方差 B、平均数 C、中位数 D、众数3. 在一个不透明的盒子中装有a个除颜色外完全相同的球，这a个球中只有3个红球，若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则a的值约为B（ ）
A、12 B、15 C、18 D、214. 下列四个函数中，y的值随着x值的增大而减小的是（ ）A、y=2x B、y=x+1 C、y= （x＞0） D、y=x2（x＞0）5. 圆内接四边形ABCD中，已知∠A=70°，则∠C=（ ）A、20° B、30° C、70° D、110°6. 如图所示的三个矩形中，是相似的是（ ）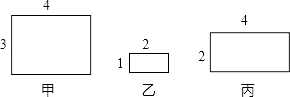
A、甲与乙 B、乙与丙 C、甲与丙 D、甲乙丙都相似7. 如图，将△ABC放在每个小正方形边长为1的网格中，点A，B，C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面半径是（ ）
A、 B、 C、2 D、8. 已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：①abc＞0，②a﹣b+c＜0，③2a+b=0，④b2﹣4ac＞0，其中正确结论个数是（ ）
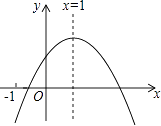A、1 B、2 C、3 D、4二、填空题
-
9. 如果在比例尺为1：1 000 000的地图上，A、B两地的图上距离是3.4厘米，那么A、B两地的实际距离是千米．
10. 若△ABC∽△A′B′C′，∠A=40°，∠C=110°，则∠B′的度数为 ．
11. 某种蔬菜按品质分成三个等级销售，销售情况如表：等级
单价（元/千克）
销售量（千克）
一等
5.0
20
二等
4.5
40
三等
4.0
40
则售出蔬菜的平均单价为元/千克．
12. 如图，转盘中8个扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 ．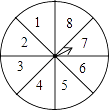
13. 如图，若点C是AB的黄金分割点，AC＞BC，AB=2，则AC的长为（结果精确到0.01）．
14. 把二次函数y=2x2的图象向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线的解析式为 ．15. 抛物线y=x2﹣8x+c的顶点在x轴上，则c的值为 ．16. 如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m，另一边减少了3m，剩余一块面积为20m2的矩形空地，若原正方形空地边长是xm，则可列方程为 ．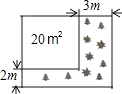
17. 如图，将正六边形ABCDEF放在直角坐标系中，中心与坐标原点重合，若A点的坐标为（﹣1，0），则点C的坐标为 ．
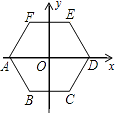18. 如图，在△ABC中，AB=6，将△ABC绕点B顺时针旋转60°后得到△DBE，点A经过的路径为弧AD，则图中阴影部分的面积是 ．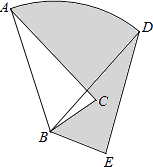
三、解答题
-
19. 解下列方程：
(1)、x2﹣6x﹣7=0；(2)、（2x+1）2=x2 ．20. 已知== ， 且x+y﹣z=6，求x、y、z的值．21. 某商场统计了今年1﹣5月A、B两种品牌冰箱的销售情况，并将获得的数据绘制成如图折线统计图：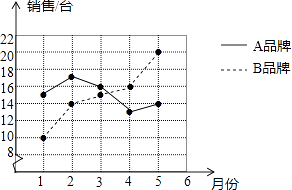
(1)、根据图中数据填写表格．
(2)、通过计算该商场这段时间内A、B两种品牌冰箱月销售量的方差，比较这两种品牌冰箱月销售量的稳定性．
22. 3张奖券中有2张是有奖的，甲、乙先后各不放回地抽取一张．
(1)、甲中奖的概率是；(2)、试用画树状图或列表法求甲、乙中奖的概率．23. 已知关于x的方程x2+2mx+m2﹣1=0(1)、试说明无论m取何值时，方程总有两个不相等的实数根；(2)、若方程有一个根为3，求2m2+12m+2016的值．24. 如图，在⊙O中，AB为直径，AC为弦，过点C作CD⊥AB于点D，将△ACD沿AC翻折，点D落在点E处，AE交⊙O于点F，连接OC、FC．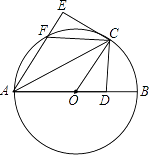
(1)、求证：CE是⊙O的切线．(2)、若FC∥AB，求证：四边形AOCF是菱形．25. 如图，抛物线的顶点D的坐标为（1，﹣4），与y轴交于点C（0，﹣3），与x轴交于A、B两点．
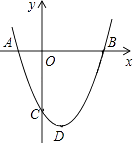(1)、求该抛物线的函数关系式；(2)、在抛物线上存在点P（不与点D重合），使得S△PAB=S△ABD ， 请求出P点的坐标．26. 某公司投资1200万元购买了一条新生产线生产新产品．根据市场调研，生产每件产品需要成本50元，该产品进入市场后不得低于80元/件且不得超过160元/件，该产品销售量y（万件）与产品售价x（元）之间的关系如图所示．
(1)、求y与x之间的函数关系式，并写出x的取值范围；
(2)、第一年公司是盈利还是亏损？求出当盈利最大或亏损最小时的产品售价；(3)、在（2）的前提下，即在第一年盈利最大或者亏损最小时，公司第二年重新确定产品售价，能否使前两年盈利总额达790万元？若能，求出第二年产品售价；若不能，说明理由．
27. 如图，直线y=﹣ x+6分别交x轴、y轴于A、B两点，抛物线y=﹣ x2+8，与y轴交于点D，点P是抛物线在第一象限部分上的一动点，过点P作PC⊥x轴于点C．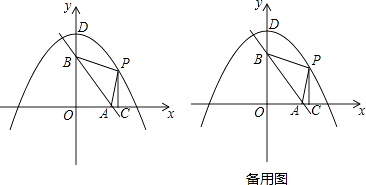
(1)、点A的坐标为 ， 点D的坐标为；(2)、探究发现：①假设P与点D重合，则PB+PC=；（直接填写答案）
②试判断：对于任意一点P，PB+PC的值是否为定值？并说明理由；
(3)、试判断△PAB的面积是否存在最大值？若存在，求出最大值，并求出此时点P的坐标；若不存在，说明理由．