内蒙古赤峰市2016-2017学年高二下学期理数期末考试试卷
试卷更新日期:2017-12-25 类型:期末考试
一、单选题
-
1. 已知复数 的实部为 ,虚部为2,则 的共轭复数是( )A、 B、 C、 D、2. 命题“ ”的否定是( )A、 B、 C、 D、3. 当 ,2,3,4,5,6时,比较 和 的大小并猜想( )A、 时, B、 时, C、 时, D、 时,4. 某产品近四年的广告费x万元与销售额y万元的统计数据如下表,

根据此表可得回归方程 中的 =9.4,据此模型预测下一年该产品广告费预算为60万元时,其销售额为( )万元.
A、650 B、655 C、677 D、7205. 五种不同的商品在货架上排成一排,其中 , 两种必须排在一起,而 , 两种不能排在一起,则不同的选排方法共有( )A、12种 B、20种 C、24种 D、48种6. 将三颗骰子各掷一次,记事件A=“三个点数都不同”, B=“至少出现一个6点”,则条件概率 , 分别等于( )A、 , B、 , C、 , D、 ,7. 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的 , 分别为63,98,则输出的 ( )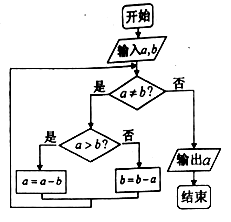 A、9 B、3 C、7 D、148. 甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是 .假设各局比赛结果相互独立.则甲队以3:2获得比赛胜利的概率为 ( )A、 B、 C、 D、9. 给定两个命题p,q,若 p是q的必要而不充分条件,则p是 q的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件10. 如图,在三棱柱 中,底面为正三角形,侧棱垂直底面, .若 分别是棱 上的点,且 , ,则异面直线 与 所成角的余弦值为( )
A、9 B、3 C、7 D、148. 甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是 .假设各局比赛结果相互独立.则甲队以3:2获得比赛胜利的概率为 ( )A、 B、 C、 D、9. 给定两个命题p,q,若 p是q的必要而不充分条件,则p是 q的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件10. 如图,在三棱柱 中,底面为正三角形,侧棱垂直底面, .若 分别是棱 上的点,且 , ,则异面直线 与 所成角的余弦值为( )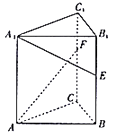 A、 B、 C、 D、11. 已知 , 分别为双曲线 : ( , )的左、右顶点, 是 上一点,且直线 , 的斜率之积为2,则 的离心率为( )A、 B、 C、 D、12. 函数 , ,若 有极大值点 ,则实数 的取值范围( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知 , 分别为双曲线 : ( , )的左、右顶点, 是 上一点,且直线 , 的斜率之积为2,则 的离心率为( )A、 B、 C、 D、12. 函数 , ,若 有极大值点 ,则实数 的取值范围( )A、 B、 C、 D、二、填空题
-
13. 已知随机变量 服从正态分布 ,且 ,则 .14. 的展开式中的常数项为 .15. 定义在 上的可导函数 ,其导函数为 满足 恒成立,则不等式 的解集为 .16. 已知直线和直线 ,抛物线 上一动点 到直线 和 的距离之和的最小值是.
三、解答题
-
17. 命题 :关于 的不等式 对一切 恒成立,命题 :指数函数 是增函数,若 或 为真、 且 为假,求实数 的取值范围.18. 某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为 .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为 ,每次中奖均可获奖金400元.
(1)、求某员工选择方案甲进行抽奖所获奖金 (元)的分布列;(2)、某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?19. 如图,在四棱锥 中, 底面 ,底面 为直角梯形, , , , 为 的中点,平面 交 于 点.、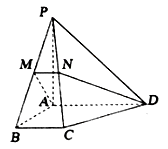 (1)、求证: ;(2)、求二面角 的余弦值.
(1)、求证: ;(2)、求二面角 的余弦值.