江苏省扬州市高邮市2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2017-12-25 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 16的平方根是（　　）

A、4 B、±4 C、﹣4 D、±8

查看试题解析
3. 点M（﹣3，2）关于y轴对称的点的坐标为（）

A、（﹣3，﹣2） B、（3，﹣2） C、（3，2） D、（﹣3，2）

查看试题解析
4. 化简 $\frac{x^{2}}{x - 1} + \frac{1}{1 - x}$ 的结果是（）

A、x+1 B、 $\frac{1}{x + 1}$ C、x﹣1 D、 $\frac{1}{x - 1}$

查看试题解析
5. 下列四组线段中，可以构成直角三角形的是（）

A、4，5，6 B、2，3，4 C、 $\sqrt{7}$ ，3，4 D、1， $\sqrt{2}$ ，3

查看试题解析
6. 如图，若BC=EC，∠BCE=∠ACD，则添加不能使△ABC≌△DBC的条件是（）

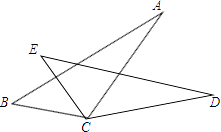A、AB=DE B、∠B=∠E C、AC=DC D、∠A=∠D

查看试题解析
7. 已知A（x₁ ， y₁），B（x₂ ， y₂）是一次函数y=2x﹣kx+1图象上的不同两个点，m=（x₁﹣x₂）（y₁﹣y₂），则当m＜0时，k的取值范围是（）

A、k＜0 B、k＞0 C、k＜2 D、k＞2

查看试题解析
8. 如图，Rt△ABC，∠ACB=90°，AC=3，BC=4，将边Ac沿CE翻折，使点A落在AB上的D处，再将边BC沿CF翻折，使点B落在CD的延长线上的点F处，两条折痕与斜边AB分别交于点E、F，则线段BF的长为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{2}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、填空题

9. 在实数1.732， $\frac{\sqrt{2}}{2}$ , $- \frac{22}{7}$ , $\sqrt[3]{- 8}$ , $\frac{π}{4}$ 中，无理数的个数为．

查看试题解析
10. 一个等腰三角形的一个角为50°，则它的顶角的度数是．

查看试题解析
11. 一次函数y=﹣2x+1的图象一定不经过第象限．

查看试题解析
12. 如图，在3×3的正方形网格中有四个格点，A、B、C、D，以其中一点为原点，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是点．

查看试题解析
13. 如图所示，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AD=2，BC=5，则△BCD的面积是．

查看试题解析
14. 一次函数y₁=kx+b与y₂=x+a的图象如图，则kx+b＞x+a的解集是．

查看试题解析
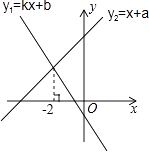15. 如图，AB=AC=AD，∠BAD=80°，则∠BCD的大小是．

查看试题解析
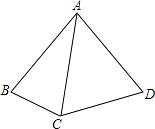16. 若关于x的方程 $\frac{2}{x - 2}$ + $\frac{x + m}{2 - x}$ =2的解为正数，则m的取值范围是．

查看试题解析
17. 已知一次函数y=kx+b，若3k﹣b=2，则它的图象一定经过的定点坐标为．

查看试题解析
18. 如图，在直角坐标系中，点A、B的坐标分别为（2，4）和（3、0）点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，在运动的过程中，当△ABC是以AB为底的等腰三角形时，此时点C的坐标为．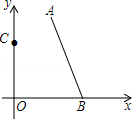

查看试题解析

三、解答题

19. 计算题

(1)、计算： $\sqrt[3]{{(- 1)}^{2}} + \sqrt[3]{- 8} + \sqrt{3} - | 1 - \sqrt{3} | + \sqrt{2}$

(2)、求x的值：25（x+2）²﹣36=0．

查看试题解析
20. 解分式方程：

(1)、 $\frac{3}{x^{2} - 9} + \frac{x}{x - 3}$ =1

(2)、2﹣ $\frac{1}{2 - x} = \frac{3 - x}{x - 2}$ ．

查看试题解析
21. 先化简： $(\frac{x + 1}{x - 1} + 1) \div \frac{x^{2} + x}{x^{2} 2 x + 1} + \frac{2 - 2 x}{x^{2} - 1}$ ，然后从﹣2≤x≤2的范围内选择一个合适的整数作为x的值代入求值．

查看试题解析
22. 春节前夕，某商店根据市场调查，用2000元购进第一批盒装花，上市后很快售完，接着又用4200元购进第二批这种盒装花．已知第二批所购的盒数是第一批所购花盒数的3倍，且每盒花的进价比第一批的进价少6元．求第一批盒装花每盒的进价．

查看试题解析
23. 如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：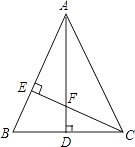

(1)、△AEF≌△CEB；

(2)、AF=2CD．

查看试题解析
24. 如图，在Rt△ABC中，∠C=90°，BD是△ABC的一条角平分线．点O、E、F分别在BD、BC、AC上，且四边形OECF是正方形．

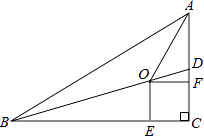(1)、求证：点O在∠BAC的平分线上；

(2)、若AC=5，BC=12，求OE的长．

查看试题解析
25. 如图，一次函数y=﹣x+m的图象和y轴交于点B，与正比例函数y= $\frac{3}{2}$ x图象交于点P（2，n）．

(1)、求m和n的值；

(2)、求△POB的面积．

查看试题解析
26. 如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）

查看试题解析
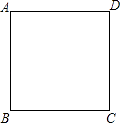27. 如图，P为正方形ABCD的边BC上一动点（P与B、C不重合），连接AP，过点B作BQ⊥AP交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交BA的延长线于点M．

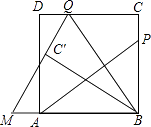(1)、试探究AP与BQ的数量关系，并证明你的结论；

(2)、当AB=3，BP=2PC，求QM的长；

(3)、当BP=m，PC=n时，求AM的长．

查看试题解析
28. 小亮和小刚进行赛跑训练，他们选择了一个土坡，按同一路线同时出发，从坡脚跑到坡顶再原路返回坡脚．他们俩上坡的平均速度不同，下坡的平均速度则是各自上坡平均速度的1.5倍．设两人出发x min后距出发点的距离为y m．图中折线表示小亮在整个训练中y与x的函数关系，其中A点在x轴上，M点坐标为（2，0）．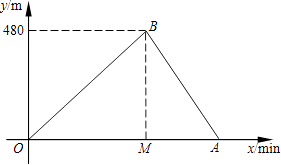

(1)、A点所表示的实际意义是； $\frac{O M}{M A}$ =；

(2)、求出AB所在直线的函数关系式；

(3)、如果小刚上坡平均速度是小亮上坡平均速度的一半，那么两人出发后多长时间第一次相遇？

查看试题解析