江苏省无锡市新区2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期:2017-12-25 类型:期末考试
一、单选题
-
1. 下面图案中是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. Rt△ABC中,∠C= ,周长为60,斜边与一条直角边之比为13∶5,这个三角形三边长分别是( )
A、1个 B、2个 C、3个 D、4个2. Rt△ABC中,∠C= ,周长为60,斜边与一条直角边之比为13∶5,这个三角形三边长分别是( )
A、5、4、3 B、13、12、5 C、10、8、6 D、26、24、103. 已知点P在第四象限,且到x轴的距离为2,则点P的坐标为( )
A、(4,-2) B、(-4,2) C、(-2,4) D、(2,-4)4. 点 、 在直线 上,若 ,则 与 大小关系是( )
A、 B、 C、 D、无法确定5. 等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )A、7 B、11 C、7或11 D、7或106. 在无锡全民健身越野赛中,甲、乙两选手的行程 y(千米)随时间(时)变化的图象(全程)如图所示.下 列四种说法: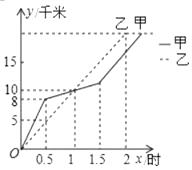
①起跑后 1 小时内,甲在乙的前面;
②第 1 小时两人都跑了 10 千米;
③甲比乙先到达终点;
④两人都跑了 20 千米.
正确的有 ( )
A、①②③④ B、①②③ C、①②④ D、②③④7. 如图,AE⊥AB且AE=AB , BC⊥CD且BC=CD , 请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )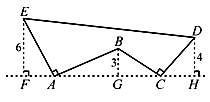 A、50 B、62 C、65 D、68
A、50 B、62 C、65 D、68二、填空题
-
8. 3184900精确到十万位的近似值是 .9. 16的算术平方根是 . 函数y= 中自变量x的取值范围是 .
10. 等腰三角形的一内角为40°,则它的底角为°.11. 若一次函数 是正比例函数.则m的值是 , 若一次函数 的图像上有两个点 , ,则m的取值范围是 .
12. 当 为 时,直线 与直线 的交点在 轴上.
13. 已知直线AB经过点A(0,5),B(2,0),若将这条直线向左平移,恰好过坐标原点,则平移后的直线解析式为 .
14.如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是 (只添一个条件即可).
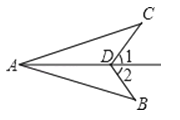 15. 如图,已知 中, , cm, cm.现将 进行折叠,使顶点 重合,则折痕 cm.
15. 如图,已知 中, , cm, cm.现将 进行折叠,使顶点 重合,则折痕 cm.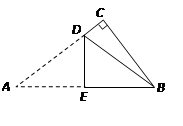 16. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为 .
16. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为 .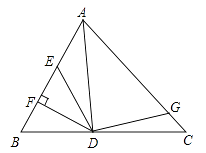 17. 如图,等腰直角三角形 ABC 中,∠BAC=90°,AB=AC,点 M,N 在边 BC 上,且∠MAN=45°.若 BM=1, CN=3,则 MN 的长为 .
17. 如图,等腰直角三角形 ABC 中,∠BAC=90°,AB=AC,点 M,N 在边 BC 上,且∠MAN=45°.若 BM=1, CN=3,则 MN 的长为 .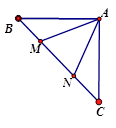
三、解答题
-
18. 计算题:
(1)、已知: 求x;(2)、计算 :19. 如图,在平面直角坐标系xOy中,点A(1,3),点B(5,1).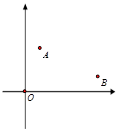 (1)、只用直尺(无刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)(2)、在(1)作出点P后,点P的坐标为 .20. 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)、只用直尺(无刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)(2)、在(1)作出点P后,点P的坐标为 .20. 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.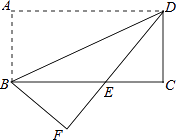 (1)、求证:△DCE≌△BFE;(2)、若 , DB=2 ,求BE的长.
(1)、求证:△DCE≌△BFE;(2)、若 , DB=2 ,求BE的长.
21. 已知:如图,△ABC中,AC=BC,∠ACB=90º,D是AC上一点,AE⊥BD交BD的延长线于E,且 求证:BD是∠ABC的平分线。 22. 南方A市欲将一批容易变质的水果运往B市销售,若有飞机、火车、汽车三种运输方式,现只选择其中一种,这三种运输方式的主要参考数据如下表所示:
22. 南方A市欲将一批容易变质的水果运往B市销售,若有飞机、火车、汽车三种运输方式,现只选择其中一种,这三种运输方式的主要参考数据如下表所示:运输工具
途中速度(km/h)
途中费用(元/km)
装卸费用(元)
装卸时间
飞机
200
16
1000
2
火车
100
4
2000
4
汽车
50
8
1000
2
若这批水果在运输(包括装卸)过程中的损耗为200元/h,记A、B两市间的距离为xkm.
(1)、如果用W1、W2、W3分别表示使用飞机、火车、汽车运输时的总支出费用(包括损耗),求W1、W2、W3与x间的关系式;(2)、当x=250时,应采用哪种运输方式,才使运输时的总支出费用最小?23. 如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t. (1)、AB= cm,AB边上的高为 cm;
(1)、AB= cm,AB边上的高为 cm;
(2)、点D在运动过程中,当△BCD为等腰三角形时,求t的值.24. 如图,已知函数 y=x+1 的图象与 y 轴交于点 A,一次函数 y=kx+b 的图象经过点 B(0,﹣1),与x 轴 以及 y=x+1 的图象分别交于点 C、D,且点 D 的坐标为(1,n),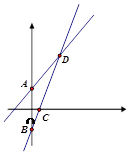 (1)、则n= ,k= ,b= ;(2)、函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(1)、则n= ,k= ,b= ;(2)、函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(3)、求四边形 AOCD 的面积;
(4)、在 x轴上是否存在点 P,使得以点 P,C,D 为顶点的三角形是直角三角形?若存在求出点 P 的坐标; 若不存在,请说明理由.25. 在△ABC中, AB、BC、AC三边的长分别为 、 、 ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.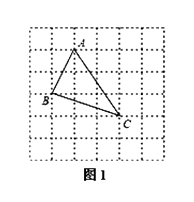 (1)、△ABC的面积为: .(2)、若△DEF三边的长分别为 、
(1)、△ABC的面积为: .(2)、若△DEF三边的长分别为 、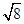 、 ,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
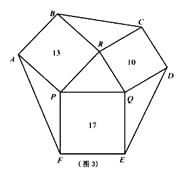
、 ,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积. (3)、如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,请利用第2小题解题方法求六边形花坛ABCDEF的面积.
(3)、如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,请利用第2小题解题方法求六边形花坛ABCDEF的面积.