江苏省无锡市锡山区2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期:2017-12-25 类型:期末考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、 B、 C、 D、2. 窗花是我国的传统艺术,下列四个窗花图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知0<a<2,则点P(a,a-2)在哪个象限( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 以下列线段长为边,能构成直角三角形的是( )A、2,3,5 B、2,3,4 C、3, ,4 D、2,4,55. 如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于 AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若∠A=25°,则∠CDB=( )
3. 已知0<a<2,则点P(a,a-2)在哪个象限( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 以下列线段长为边,能构成直角三角形的是( )A、2,3,5 B、2,3,4 C、3, ,4 D、2,4,55. 如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于 AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若∠A=25°,则∠CDB=( ) A、25° B、50° C、60° D、90°6. 一次函数y=-2x-1的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下列两个三角形中,一定全等的是( )A、两个等腰三角形 B、两个等腰直角三角形 C、两个等边三角形 D、两个周长相等的等边三角形8. 已知点A(m+2,3m-6)在第一象限角平分线上,则m的值为( )A、2 B、-1 C、4 D、-29. 已知一次函数y=kx+b中,x取不同值时,y对应的值列表如下:
A、25° B、50° C、60° D、90°6. 一次函数y=-2x-1的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下列两个三角形中,一定全等的是( )A、两个等腰三角形 B、两个等腰直角三角形 C、两个等边三角形 D、两个周长相等的等边三角形8. 已知点A(m+2,3m-6)在第一象限角平分线上,则m的值为( )A、2 B、-1 C、4 D、-29. 已知一次函数y=kx+b中,x取不同值时,y对应的值列表如下:x
…
-m2-1
2
3
…
y
…
-1
0
n2+1
…
则不等式kx+b>0(其中k,b,m,n为常数)的解集为( )
A、x>2 B、x>3 C、x<2 D、无法确定10. 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )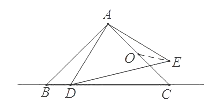 A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
11. 4是的算术平方根.12. 无锡地铁3号线预计全长约42500米,将42500用科学记数法表示为 .13. 点P(-2,3)关于x轴的对称点的坐标是 .14. 如图,△ABC中,AB=AC,点D,E在BC边上,若要以“SAS”为依据说明△ABD≌△ACE,还要添加的条件为 .
 15. 如图,已知函数y1=kx-1和y2=x-b的图象交于点P(-2,-5),则根据图象可得不等式kx-1>x-b的解集是 .
15. 如图,已知函数y1=kx-1和y2=x-b的图象交于点P(-2,-5),则根据图象可得不等式kx-1>x-b的解集是 .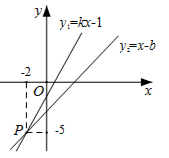 16. 如图,在平面直角坐标系中,已知点A(0,4),B(-3,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为 .
16. 如图,在平面直角坐标系中,已知点A(0,4),B(-3,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为 . 17. 若直线l1:y=ax+b(a≠0)与直线l2:y=mx+n (m≠0)的交点坐标为(-2,1),则直线l3:y=a(x-3)+b+2(a≠0)与直线l4:y=m(x-3)+n+2(m≠0)的交点坐标为 .
17. 若直线l1:y=ax+b(a≠0)与直线l2:y=mx+n (m≠0)的交点坐标为(-2,1),则直线l3:y=a(x-3)+b+2(a≠0)与直线l4:y=m(x-3)+n+2(m≠0)的交点坐标为 .
三、解答题
-
18. 计算题
(1)、计算:(2)、求(x-2)3=27中x的值.19. 已知:如图,AB∥CD,E是AB的中点,CE=DE.求证: (1)、∠AEC=∠BED;(2)、AC=BD.20. 方格纸中小正方形的顶点叫格点.点A和点B是格点,位置如图.
(1)、∠AEC=∠BED;(2)、AC=BD.20. 方格纸中小正方形的顶点叫格点.点A和点B是格点,位置如图.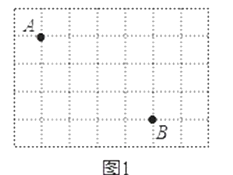 (1)、在图1中确定格点C使△ABC为直角三角形,画出一个这样的△ABC;
(1)、在图1中确定格点C使△ABC为直角三角形,画出一个这样的△ABC;
(2)、在图2中确定格点D使△ABD为等腰三角形,画出一个这样的△ABD; (3)、在图2中满足题(2)条件的格点D有个.
(3)、在图2中满足题(2)条件的格点D有个.
21. 我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:销售方式
批发
零售
利润(元/kg)
6
12
设按计划全部售出后的总利润为y元,其中批发量为xkg.
(1)、求y与x之间的函数关系式;(2)、若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.22. 如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.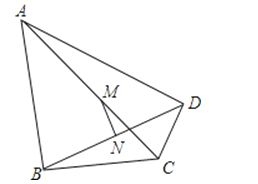 23. 阅读下面材料:
23. 阅读下面材料:小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.

小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).
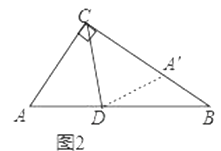
请回答:
(1)、在图2中,小明得到的全等三角形是△≌△;
(2)、求BC和AC、AD之间的数量关系是
(3)、参考小明思考问题的方法,解决问题:如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.
 24. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.
24. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.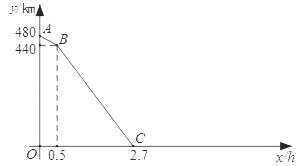 (1)、由图象知,慢车的速度为km/h,快车的速度为km/h;
(1)、由图象知,慢车的速度为km/h,快车的速度为km/h;
(2)、请在图中补全函数图象;
(3)、求当x为多少时,两车之间的距离为300km.
25. 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.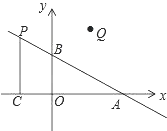 (1)、当b=3时,
(1)、当b=3时,①求直线AB的解析式;
②若QO=QA,求P点的坐标.
(2)、是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.