江苏省无锡市南长区2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期:2017-12-25 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在-0.1, , , , ,0中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个3. 下列给出的三条线段的长,其中能组成直角三角形的是( )A、62、82、102 B、6、8、9 C、2、 、 D、 、 、4. 下列说法:
2. 在-0.1, , , , ,0中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个3. 下列给出的三条线段的长,其中能组成直角三角形的是( )A、62、82、102 B、6、8、9 C、2、 、 D、 、 、4. 下列说法:①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③- 是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
A、0个 B、1 C、2个 D、3个5. 有一个等腰三角形的周长为16,其中一边长为4,则这个等腰三角形的底边长为( )A、4 B、6 C、4或8 D、86. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )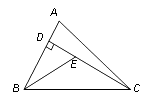 A、5 B、7 C、10 D、37. 直线y=kx+b不经过第三象限,则k、b应满足( )A、k>0,b<0 B、k<0,b>0 C、k<0 b<0 D、k<0,b≥08. 父亲节,学校“文苑”专栏登出了某同学回忆父亲的小诗:“同辞家门赴车站,别时叮咛语千万,学子满载信心去,老父怀抱希望还.”如果用纵轴y表示父亲和学子在行进中离家的距离,横轴t表示离的时间,那么下面与上述诗意大致相吻合的图象是( )
A、5 B、7 C、10 D、37. 直线y=kx+b不经过第三象限,则k、b应满足( )A、k>0,b<0 B、k<0,b>0 C、k<0 b<0 D、k<0,b≥08. 父亲节,学校“文苑”专栏登出了某同学回忆父亲的小诗:“同辞家门赴车站,别时叮咛语千万,学子满载信心去,老父怀抱希望还.”如果用纵轴y表示父亲和学子在行进中离家的距离,横轴t表示离的时间,那么下面与上述诗意大致相吻合的图象是( )
A、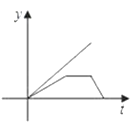 B、
B、 C、
C、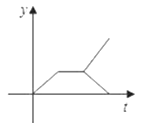 D、
D、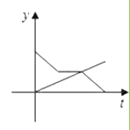 9. 如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )
9. 如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( ) A、5对 B、6对 C、7对 D、8对10. 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
A、5对 B、6对 C、7对 D、8对10. 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )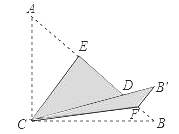 A、 B、6 C、 D、
A、 B、6 C、 D、二、填空题
-
11. 25的平方根是;64的立方根是 .12. 用四舍五入法把17.8961精确到百分位,得到的近似值是 .13. 如果等腰三角形的一个外角是105°,那么它的顶角的度数为 .
14. 若点P(3,m)与Q(n,-6)关于x轴对称,则m+n= .15. 在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为 .16. 如图,l1:y=x+1和l2:y=mx+n相交于P(a,2),则x+1≥mx+n解集为 . 17. 如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,∠3=°.
17. 如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,∠3=°.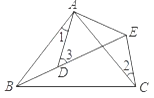 18. 如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=9,DE=7.5,则CD的长为 .
18. 如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=9,DE=7.5,则CD的长为 . 19. 如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
19. 如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
三、解答题
-
20. 解方程:
(1)、4x2-16=0;(2)、 (x-2)3=18.21. 计算:(1)、 ;(2)、(- )2+|1- |+(- )-1 .22. 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.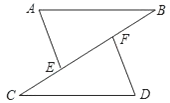 (1)、求证:AB=CD;(2)、若AB=CF,∠B=40°,求∠D的度数.23. 我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
(1)、求证:AB=CD;(2)、若AB=CF,∠B=40°,求∠D的度数.23. 我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.运用上述知识,解决下列问题:
(1)、如果(a+2) -b+3=0,其中a、b为有理数,那么a= , b=;
(2)、如果2b-a-(a+b-4) =5,其中a、b为有理数,求3a+2b的平方根.
24. 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE. (1)、在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点,并求出BF的长;
(1)、在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点,并求出BF的长;
(2)、△AEF与四边形ABCD重叠部分的面积为 .
25. 如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=6,求线段DE的长. 26. 如图,直线l1的解析表达式为y=- x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
26. 如图,直线l1的解析表达式为y=- x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C. (1)、求直线l2的函数关系式;(2)、求△ADC的面积;(3)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标.27. 如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
(1)、求直线l2的函数关系式;(2)、求△ADC的面积;(3)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标.27. 如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0). (1)、若点P在AC上,且满足PA=PB时,求出此时t的值;
(1)、若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)、若点P恰好在∠BAC的角平分线上,求t的值;(3)、在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
28. 如图1,某物流公司恰好位于连接A,B两地的一条公路旁的C处.某一天,该公司同时派出甲.乙两辆货车以各自的速度匀速行驶.其中,甲车从公司出发直达B地;乙车从公司出发开往A地,并在A地用1h配货,然后掉头按原速度开往B地.图2是甲.乙两车之间的距离S(km)与他们出发后的时间x(h)之间函数关系的部分图象. (1)、由图象可知,甲车速度为km/h;乙车速度为km/h.
(1)、由图象可知,甲车速度为km/h;乙车速度为km/h.
(2)、已知最终乙车比甲车早到B地0.5h,求甲车出发1.5h后直至到达B地的过程中,S与x的函数关系式及x的取值范围,并在图2中补全函数图象.