江苏省无锡市滨湖区2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期：2017-12-25 类型：期末考试
一、单选题
-
1. 的值为（ ）A、 B、 C、5 D、252. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 在－0.101001，
， 
，－ 
，0中，无理数的个数是（ ） A、1个 B、2个 C、3个 D、4个4. 若 ，且 ， 为相邻的整数，则 的值为（ ）A、2 B、3 C、4 D、55. 下列四组线段中，可以构成直角三角形的是（ ）A、4cm、5cm、6cm B、1cm、 cm、3cm C、2cm、3cm、4cm D、1.5cm、2cm、2.5cm6. 已知点A ， ），B（2， 都在直线 上，则 、 大小关系是（ ）
A、 B、 C、 D、不能比较7. 如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）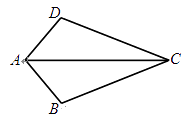
A、CB＝CD B、∠BAC＝∠DAC C、∠BCA＝∠DCA D、∠B＝∠D＝90°8. 如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm 至D点，则橡皮筋被拉长了（ ）
A、4cm B、3cm C、2cm D、5cm9. 如图，正方形网格中的每个小正方形边长都是1．已知A、B是两格点，若△ABC为等腰三角形，且S△ABC＝1.5，则满足条件的格点C有（ ）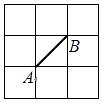
A、1个 B、2个 C、3个 D、4个10. 如图，直线y＝x―4与y轴、x轴分别交于点A、B，点C为双曲线y＝ 上一点，OC∥AB，连接BC交双曲线于点D，点D恰好是BC的中点，则k的值是（ ）
A、 B、2 C、4 D、二、填空题
-
11. 如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（4，8），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E，那么点D的坐标为 ．
12. 点A（－3，2）关于 轴对称的点的坐标为 ．13. 据统计，2015年国庆期间，无锡灵山风景区某一天接待游客的人数为19800人次，将这个数字精确到千位，并用科学记数法表示为 ．
14. 若等腰三角形的两边长为2和5，则它的周长为 ．15. 在平面直角坐标系中，把直线 沿y轴向上平移两个单位后，得到的直线的函数关系式为 ．16. 如图，点A在双曲线y＝ （x＞0）上，点B在双曲线y＝ （x＞0）上，且AB∥y轴，点P是y轴上的任意一点，则△PAB的面积为 ．
17. 甲、乙二人从学校出发去科技馆，甲步行一段时间后，乙骑自行车沿相同路线行进，两人均匀速前行，他们的路程差s（米）与甲出发时间t（分）之间的函数关系如图所示．下列说法：①乙先到达青少年宫；②乙的速度是甲速度的2.5倍；③b＝480；④a＝24．其中正确的是（填序号）.
三、解答题
-
18. 计算题
(1)、计算：(2)、已知： ，求 .19. 如图，在平面直角坐标系xOy中，点A（0，8）、点B（6，8）.点P同时满足下面两个条件：①点P到A、B两点的距离相等；②点P到∠xOy的两边的距离相等.
(1)、只用直尺（没有刻度）和圆规，作出符合要求的点P（作图痕迹清楚，不必写出作法）；(2)、在（1）作出点P后，写出点P的坐标.20. 如图，已知：△ABC中，AB＝AC，M、D、E分别是BC、AB、AC的中点．
(1)、求证：MD＝ME；(2)、若MD＝3，求AC的长.21. 如图，△ABC中，∠A＝36°，∠C＝72°，∠DBC＝36°.
(1)、求∠1的度数；(2)、求证：BC＝BD＝AD.22. 如图，小区A与公路l的距离AC＝200米，小区B与公路l的距离BD＝400米，已知CD＝800米，现要在公路旁建造一利民超市P，使P到A、B两小区的路程之和最短，超市应建在哪？
(1)、请在图中画出点P；
(2)、求CP的长度；
(3)、求PA＋PB的最小值.
23. 如图在平面直角坐标系xOy中，反比例函数y1＝ （x＞0）的图象与一次函数y2＝kx－k的图象的交点为A（m，2）．
(1)、求一次函数的解析式；(2)、观察图像，直接写出使y1≥y2的x的取值范围．(3)、设一次函数y＝kx－k的图象与y轴交于点B，若点P是x轴上一点，且满足△PAB的面积是4，请写出点P的坐标．24. 小林家、小华家与图书馆依次在一条直线上．小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书，已知小林到达图书馆花了20分钟．设两人出发x（分钟）后，小林离小华家的距离为y（米），y与x的函数关系如图所示．
(1)、小林的速度为米/分钟，a＝ ， 小林家离图书馆的距离为米；(2)、已知小华的步行速度是40米/分钟，设小华步行时与家的距离为y1（米），请在图中画出y1（米）与x（分钟 ）的函数图象；
(3)、小华出发几分钟后两人在途中相遇？
25. 如图1，正方形ABCD的边长为4厘米，E为AD边的中点，F为AB边上一点，动点P从点B出发，沿B→C→D→E，向终点E以每秒a厘米的速度运动，设运动时间为t秒，△PBF的面积记为S. S与t的部分函数图象如图2所示，已知点M（1， ）、N（5，6）在S与t的函数图象上.
(1)、求线段BF的长及a的值；
(2)、写出S与t的函数关系式，并补全该函数图象；
(3)、当t为多少时，△PBF的面积S为4.
26. 模型建立：如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于D，过B作BE⊥ED于E．
(1)、求证：△BEC≌△CDA；(2)、模型应用：①已知直线l1：y＝－ x－4与y轴交于A点，将直线l1绕着A点逆时针旋转45°至l2 ， 如图2，求l2的函数解析式；
②如图3，矩形ABCO，O为坐标原点，B的坐标为（8，－6），A、C分别在坐标轴上，P是线段BC上动点，设PC＝m，已知点D在第四象限，且是直线y＝－2x＋6上的一点，若△APD是不以点A为直角顶点的等腰Rt△，请求出点D的坐标．