江苏省无锡江阴市2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2017-12-25 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、3 B、－3 C、±3 D、± $\sqrt{3}$

查看试题解析
2. 下列各数： $π$ ， $\frac{4}{3}$ ，0，－1中，无理数是（）

A、 $π$ B、 $\frac{4}{3}$ C、0 D、－1

查看试题解析
3. 下列图形中，轴对称图形的个数为（）

A、1个 B、2 个 C、3个 D、4个

查看试题解析
4. 点P（ 2，－3）关于x轴对称的点是（）

A、（－2， 3） B、（2，3） C、（－2，－3） D、（2，－3）

查看试题解析
5. 下列各组数中，不能作为直角三角形三边长度的是（）

A、2、3、4 B、3、4、5 C、6、8、10 D、25、24、7

查看试题解析
6. 下列条件中，能判定两个直角三角形全等的是（）

A、斜边相等 B、面积相等 C、两锐角对应相等 D、两直角边对应相等

查看试题解析
7. 已知一次函数y＝（m＋3）x－2中，y的值随x的增大而增大，则m的取值范围是（）

A、m＞0 B、m＜0 C、m＞－3 D、m＜－3

查看试题解析
8. 如图，在△ABC中，D为BC上一点，且AB＝AD＝DC，∠B＝80°，则∠C等于（）

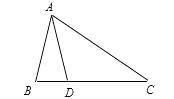A、20° B、30° C、40° D、50°

查看试题解析
9. 如图，AD＝AB＝BC，那么∠1和∠2之间的关系是（）

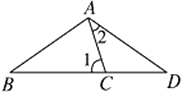A、∠1＝∠2 B、2∠1+∠2＝180° C、∠1+3∠2＝180° D、3∠1－∠2＝180°

查看试题解析
10. 甲、乙两辆摩托车分别从A、B两地出发相向而行，图中 $l_{1}$ 、 $l_{2}$ 分别表示两辆摩托车与A地的距离s（千米）与行驶时间t（小时）之间的函数关系，则下列说法：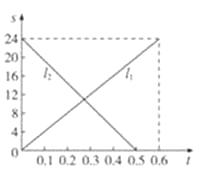

①A、B两地相距24千米；
②甲车比乙车行完全程多用了0.1小时；
③甲车的速度比乙车慢8千米／时；
④两车出发后，经过 $\frac{3}{11}$ 小时，两车相遇．
其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{64}$ = ．

查看试题解析
12. 已知点A（a－1，2+a）在第二象限，那么a的取值范围是．

查看试题解析
13. 已知一个直角三角形的两条直角边分别为6和8，则它斜边上的中线的长为．

查看试题解析
14. 已知一个等腰三角形的顶角为100°，则它的底角为．

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE=cm．

查看试题解析
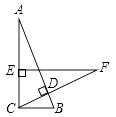16. 如图，函数y=2x和y=ax+4的图象相交于点A（1，m），则不等式2x＜ax+4的解集为．

查看试题解析
17. 如图所示，等边△ABC中，B点在坐标原点，C点坐标为（4，0），点A关于x轴对称点A′的坐标为．

查看试题解析
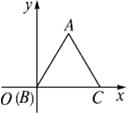18. 如图是一个围棋棋盘的局部，若把这个围棋棋盘放置在一个平面直角坐标系中，白棋①的坐标是（-2，-2），白棋③的坐标是（-1，-4），则黑棋②的坐标是．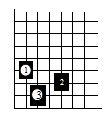

查看试题解析

三、解答题

19. 计算

(1)、（﹣1）²⁰¹⁵﹣ $| - \sqrt{3} |$ + $\sqrt{12}$ +（ $\sqrt{3}$ ﹣π）⁰；

(2)、 ${(\sqrt{3} - 1)}^{2} - （ 3 + \sqrt{5} ）$ $（ 3 - \sqrt{5} ）$

查看试题解析
20. 已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数 $y = \frac{1}{2} x$ 的图象相交于点（2，a）．

(1)、求a的值．

(2)、求一次函数y=kx+b的表达式．

(3)、在同一坐标系中，画出这两个函数的图象．

查看试题解析
21. 化简求值：

(1)、已知x＝ $\sqrt{2}$ －1，求x²＋3x－1的值；

(2)、已知 $a = - 2 - \sqrt{3} ， b = \sqrt{3} - 2$ ，求 ${(a + b)}^{2} + (a - b) (2 a + b) - 3 a^{2}$ 值．

查看试题解析
22. 已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．

查看试题解析
23. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．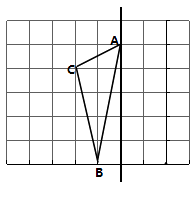

(1)、在图中画出与△ABC关于直线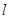成轴对称的△A ；

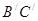(2)、线段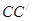被直线；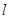

(3)、在直线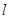上找一点P，使PB+PC的长最短，并算出这个最短长度．

查看试题解析
24. 探索与研究：
方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以
∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；

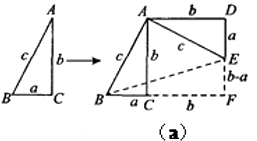
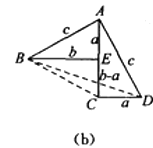
方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？

查看试题解析
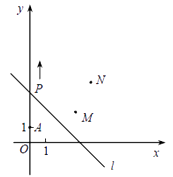
25. 如图，A（0，1），M（3，2），N（4，4），动点P从点A出发，沿y
轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为 t 秒．（直线y = kx+b平移时k不变）

(1)、当t＝3时，求 l 的解析式；

(2)、若点M，N位于l 的异侧，确定 t 的取值范围．

查看试题解析
26. 如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，
∠BAD＝45°，AD与BE交于点F，连接CF．

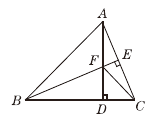(1)、求证：BF＝2AE；

(2)、若CD＝ $\sqrt{2}$ ，求AD的长．

查看试题解析
27. 钓鱼岛是我国渤海海峡上的一颗明珠，渔产丰富．一天某渔船离开港口前往该海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向钓鱼岛驶来，渔船向渔政部门报告，并立即返航．渔政船接到报告后，立即从该港口出发赶往钓鱼岛．下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象．（假设渔船与渔政船沿同一航线航行）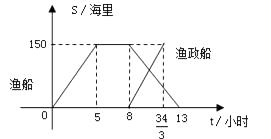

(1)、直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式．

(2)、求渔船和渔政船相遇时，两船与钓鱼岛的距离．

(3)、在渔政船驶往钓鱼岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？

查看试题解析