江苏省泰州市靖江市2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2017-12-25 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示4个汉字中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若a＞0，b＜﹣2，则点（a，b+2）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 使分式 $\frac{2 x + 1}{2 x - 1}$ 无意义的x的值是（）

A、x=﹣ $\frac{1}{2}$ B、x= $\frac{1}{2}$ C、x≠﹣ $\frac{1}{2}$ D、x≠ $\frac{1}{2}$

查看试题解析
4. 如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（）

A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA

查看试题解析
5. 一次函数y=mx+|m﹣1|的图象过点（0，2），且y随x的增大而增大，则m的值为（）

A、﹣1 B、1 C、3 D、﹣1或3

查看试题解析
6. 甲、乙两人沿相同的路线由A地到B地匀速前进，A，B两地间的路程为20千米，他们前进的路程为s（单位：千米），甲出发后的时间为t（单位：小时），甲、乙前进的路程与时间的函数图象如图所示．根据图象信息，下列说法正确的是（）

A、甲的速度是4千米/小时 B、乙的速度是10千米/小时 C、甲比乙晚到B地3小时 D、乙比甲晚出发1小时

查看试题解析

二、填空题

7. 已知函数y=（n﹣2）x+n²﹣4是正比例函数，则n为．

查看试题解析
8. 点C到x轴的距离为1，到y轴的距离为3，且在第三象限，则C点坐标是．

查看试题解析
9. 化简： $\sqrt{8}$ ﹣ $\sqrt{2}$ = ．

查看试题解析
10. 已知 $x + \frac{1}{x} = 3$ ，则代数式 $x^{2} + \frac{1}{x^{2}}$ 的值为．

查看试题解析
11. 在等腰△ABC中，AB=AC，其周长为20cm，则AB边的取值范围是cm．

查看试题解析
12. 如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是．

查看试题解析
13. 如图，△ABC是等边三角形，点D为AC边上一点，以BD为边作等边△BDE，连接CE．若CD=1，CE=3，则BC= ．

查看试题解析
14. 如图，已知函数y=3x+b和y=ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是．

查看试题解析
15. 当x分别取﹣ $\frac{1}{2017}$ 、﹣ $\frac{1}{2016}$ 、﹣ $\frac{1}{2015}$ 、…、﹣ $\frac{1}{2}$ 、﹣2、﹣1、0、1、2、…、2015、2016、2017时，计算分式 $\frac{x^{2} - 1}{x^{2} + 1}$ 的值，再将所得结果相加，其和等于．

查看试题解析

三、解答题

16. 计算： $\sqrt{8}$ $+ {(\frac{1}{2})}^{- 1} - {(π + 2)}^{0}$ +|1+ $\sqrt{2}$ |．

查看试题解析
17. 解方程： $\frac{x}{x - 1}$ =1+ $\frac{2}{x}$ ．

查看试题解析
18. 如图，正方形网格中的每个小正方形边长都是1．

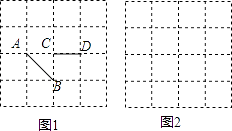(1)、图1中已知线段AB、CD，画线段EF，使它与AB、CD组成轴对称图形（要求：画出一个即可）；

(2)、在图2中画出一个以格点为端点长为 $\sqrt{13}$ 的线段．

查看试题解析
19. 已知：y﹣3与x成正比例，且当x=﹣2时，y的值为7．

(1)、求y与x之间的函数关系式；

(2)、若点（﹣2，m）、点（4，n）是该函数图象上的两点，试比较m、n的大小，并说明理由．

查看试题解析
20. 在Rt△ABC中，∠ACB=90°，AC=BC，D为BC中点，CE⊥AD于E，BF∥AC交CE的延长线于F．

(1)、求证：△ACD≌△CBF；

(2)、求证：AB垂直平分DF．

查看试题解析
21. 先化简，再求值：（ $\frac{x}{x + 2}$ ﹣ $\frac{x^{2} - 4 x + 4}{x^{2} - 4}$ ）÷ $\frac{x}{x + 2}$ ，其中x= $\sqrt{2}$ ．

查看试题解析
22. 如图所示，“赵爽弦图”由4个全等的直角三角形拼成，在Rt△ABC中，∠ACB=90°，AC=b，BC=a，请你利用这个图形解决下列问题：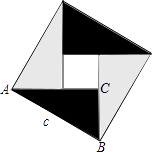

(1)、证明勾股定理；

(2)、说明a²+b²≥2ab及其等号成立的条件．

查看试题解析
23. 已知直线l₁：y=﹣ $\frac{3}{4} x + 3$ 与直线l₂：y=kx﹣ $\frac{16}{3}$ 交于x轴上的同一个点A，直线l₁与y轴交于点B，直线l₂与y轴的交点为C．

(1)、求k的值，并作出直线l₂图象；

(2)、若点P是线段AB上的点且△ACP的面积为15，求点P的坐标；

(3)、若点M、N分别是x轴上、线段AC上的动点（点M不与点O重合），是否存在点M、N，使得△ANM≌△AOC？若存在，请求出N点的坐标；若不存在，请说明理由．

查看试题解析
24. 在△ABC中，∠BAC=90°，AB=AC，在△ABC的外部作∠ACM，使得∠ACM= $\frac{1}{2}$ ∠ABC，点D是直线BC上的动点，过点D作直线CM的垂线，垂足为E，交直线AC于F．

(1)、如图1所示，当点D与点B重合时，延长BA，CM交点N，证明：DF=2EC；

(2)、当点D在直线BC上运动时，DF和EC是否始终保持上述数量关系呢？请你在图2中画出点D运动到CB延长线上某一点时的图形，并证明此时DF与EC的数量关系．

查看试题解析