江苏省淮安市淮安区八年级上学期数学期末考试试卷

试卷更新日期：2017-12-25 类型：期末考试

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列各式中正确的是（）

A、 $\sqrt{16}$ =±4 B、 $\sqrt[3]{- 27} = - 9$ C、 $\sqrt[3]{{(- 3)}^{2}} = - 3$ D、 $\sqrt{2 \frac{1}{4}} = 1 \frac{1}{2}$

查看试题解析
3. 下列四组线段中，不能组成直角三角形的是（）

A、a=3，b=4，c=3 B、a= $\sqrt{2}$ ，b= $\sqrt{3}$ ，c= $\sqrt{5}$ C、a=3，b=4，c= $\sqrt{7}$ D、a=1，b= $\sqrt{2}$ ，c=3

查看试题解析
4. 在△ABC和△DEF中，给出下列四组条件：
①AB=DE，BC=EF，AC=DF；
②AB=DE，∠B=∠E，BC=EF；
③∠B=∠E，BC=EF，AC=DF；
④∠A=∠D，∠B=∠E，∠C=∠F．
其中，能使△ABC≌△DEF的条件共有（）

A、1组 B、2组 C、3组 D、4组

查看试题解析
5. 已知点P关于y轴的对称点P₁的坐标是（2，3），则点P坐标是（）

A、（﹣3，﹣2） B、（﹣2，3） C、（2，﹣3） D、（3，﹣2）

查看试题解析
6. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝8，DE＝5，则△BCE的面积等于（）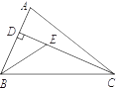

A、20 B、7 C、5 D、4

查看试题解析
7. 八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（）

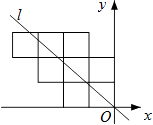A、y=﹣x B、y=﹣ $\frac{3}{4}$ x C、y=﹣ $\frac{3}{5}$ x D、y=﹣ $\frac{9}{10}$ x

查看试题解析
8. 等腰三角形的周长为16cm，其中一边长为4cm，则该等腰三角形底长上的高为（）

A、4cm或8cm B、4cm或6cm C、6cm D、 $\sqrt{32}$ cm

查看试题解析

二、填空题

9. 27的立方根为．

查看试题解析
10. 小亮的体重为43.90kg，精确到1kg得到的近似数为．

查看试题解析
11. 一个角的对称轴是它的．

查看试题解析
12. 在平面直角坐标系，点A（﹣1，﹣2），B（3，﹣4），C（3，0），D（0，﹣2），E（﹣2，5），F（3，1），G（0，2），H（﹣3，0）中，第二象限的点有个．

查看试题解析
13. 已知y与x成正比，当x=﹣3时，y=2，则y与x之间的函数关系式为．

查看试题解析
14. 如图所示，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却踩伤了花草．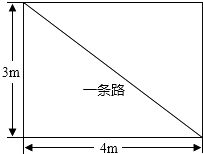

查看试题解析
15. 点（﹣1，y₁）、（2，y₂）是直线y=﹣2x+1上的两点，则y₁y₂（填“＞”或“=”或“＜”）

查看试题解析
16. 如图，已知△ABC和△BDE均为等边三角形，连接AD、CE，若∠BAD=39°，那么∠BCE=度．

查看试题解析
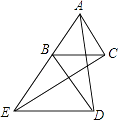17. 如图，一次函数y=kx+b的图象与正比例函数y=2x的图象平行，且经过点A（1，﹣2），则kb= ．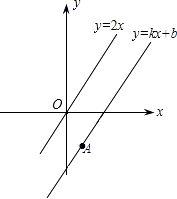

查看试题解析

三、解答题

18. 如图，点D、E分别在△ABC的边BC、AC上，且AB=AC，AD=AE．

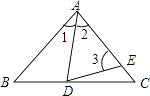
①当∠B为定值时，∠CDE为定值；
②当∠1为定值时，∠CDE为定值；
③当∠2为定值时，∠CDE为定值；
④当∠3为定值时，∠CDE为定值；
则上述结论正确的序号是．

查看试题解析
19. 计算题

(1)、求x的值：x²=25

(2)、计算： $\sqrt{{(- 2)}^{2}}$ ﹣ $\sqrt[3]{8}$ + $\sqrt{16}$ ．

查看试题解析
20. 在平面直角坐标系中有点M（m，2m+3）．

(1)、若点M在x轴上，求m的值；

(2)、若点M在第三象限内，求m的取值范围；

(3)、点M在第二、四象限的角平分线上，求m的值．

查看试题解析
21. 如图，点D、B在AF上，AD=FB，AC=EF，∠A=∠F．求证：∠C=∠E．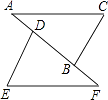

查看试题解析
22. 如图，已知A（﹣2，3）、B（4，3）、C（﹣1，﹣3）．

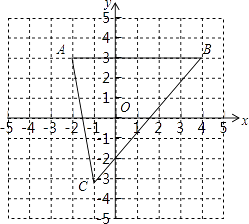(1)、求点C到x轴的距离；

(2)、分别求△ABC的三边长；

(3)、点P在y轴上，当△ABP的面积为6时，请直接写出点P的坐标．

查看试题解析
23. 已知：如图，AB∥CD，E是AB的中点，∠CEA=∠DEB．

(1)、试判断△CED的形状并说明理由；

(2)、若AC=5，求BD的长．

查看试题解析
24. 一次函数y=kx+4的图象经过点（﹣3，﹣2）．

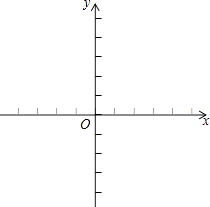(1)、求这个函数表达式；

(2)、画出该函数的图象．

(3)、判断点（3，5）是否在此函数的图象上．

查看试题解析
25. 已知某校有一块四边形空地ABCD如图，现计划在该空地上种草皮，经测量∠A=90°，AB=3cm，BC=12cm，CD=13cm，DA=4cm．若种每平方米草皮需100元，问需投入多少元？

查看试题解析
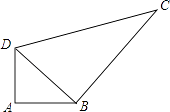26. 小丽的家和学校在一条笔直的马路旁，某天小丽沿着这条马路上学，先从家步行到公交站台甲，再乘车到公交站台乙下车，最后步行到学校（在整个过程中小丽步行的速度不变），图中折线ABCDE表示小丽和学校之间的距离y（米）与她离家时间x（分钟）之间的函数关系．

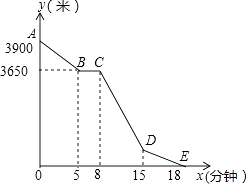(1)、求小丽步行的速度及学校与公交站台乙之间的距离；

(2)、当8≤x≤15时，求y与x之间的函数关系式．

查看试题解析
27. 已知在长方形ABCD中，AB=4，BC= $\frac{25}{2}$ ，O为BC上一点，BO= $\frac{7}{2}$ ，如图所示，以BC所在直线为x轴，O为坐标原点建立平面直角坐标系，M为线段OC上的一点．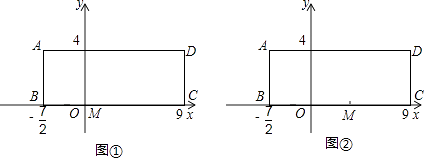

(1)、若点M的坐标为（1，0），如图①，以OM为一边作等腰△OMP，使点P在y轴上，则符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标；

(2)、若点M的坐标为（1，0），如图①，以OM为一边作等腰△OMP，使点P落在长方形ABCD的一边上，则符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标．

(3)、若将（2）中的点M的坐标改为（4，0），其它条件不变，如图②，那么符合条件的等腰三角形有几个？求出所有符合条件的点P的坐标．

查看试题解析