江苏省常州市2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期:2017-12-25 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 =2 B、 =﹣2 C、 =±2 D、 =±22. 若一个三角形的三边长分别为6、8、10,则这个三角形最长边上的中线长为( )A、3.6 B、4 C、4.8 D、53. 已知一次函数y=kx+b,函数值y随自变置x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
A、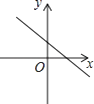 B、
B、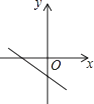 C、
C、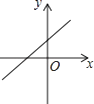 D、
D、 4. 如图,下列条件中,不能证明△ABC≌△DCB的是( )
4. 如图,下列条件中,不能证明△ABC≌△DCB的是( ) A、AB=CD,AC=BD B、AB=CD,∠ABC=∠BCD C、∠ABC=∠DCB,∠A=∠D D、AB=CD,∠A=∠D5. 如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若∠BAC=110°,则∠EAF为( )
A、AB=CD,AC=BD B、AB=CD,∠ABC=∠BCD C、∠ABC=∠DCB,∠A=∠D D、AB=CD,∠A=∠D5. 如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若∠BAC=110°,则∠EAF为( ) A、35° B、40° C、45° D、50°6. 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
A、35° B、40° C、45° D、50°6. 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )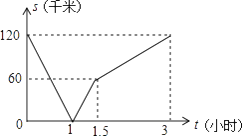
①A,B两地相距60千米:
②出发1小时,货车与小汽车相遇;
③出发1.5小时,小汽车比货车多行驶了60千米;
④小汽车的速度是货车速度的2倍.
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 36的平方根是 , 81的算术平方根是 .8. ﹣2的相反数是 , 绝对值是 .9. 在实数﹣7,0.32, , , , ﹣中,无理数有 个.10. 若点(m,3)在函数y=﹣ x+2的图象上,则m= .11. 已知点P的坐标为(﹣2,3),若点Q与点P关于x轴对称,则点Q的坐标为 .
12. 点(﹣4,y1),(2,y2)都在直线y=﹣ x+2上,则y1y2(填“>”或“<”)13. 如图,在等边△ABC中,D、E分别是AB、AC上的点,且AD=CE,则∠BCD+∠CBE=度. 14. 如图,在△ABC中,AD⊥BC,D为BC的中点,∠BAC=50°,则△ABD≌ , ∠B=度.
14. 如图,在△ABC中,AD⊥BC,D为BC的中点,∠BAC=50°,则△ABD≌ , ∠B=度. 15. 如图,在△ABC中,∠C=90°,AD平分∠CAB,AC=3,AD=4,则点D到直线AB的距离是 .
15. 如图,在△ABC中,∠C=90°,AD平分∠CAB,AC=3,AD=4,则点D到直线AB的距离是 . 16. 如图.过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称,过点A2作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称.过点A3作x轴的垂线,交直线y=2x于点B3;…按此规律作下去.则点A3的坐标为 , 点Bn的坐标为 .
16. 如图.过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称,过点A2作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称.过点A3作x轴的垂线,交直线y=2x于点B3;…按此规律作下去.则点A3的坐标为 , 点Bn的坐标为 .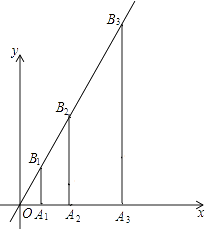
三、解答题
-
17. 已知:3x2=27,求x的值.18. 计算: +π0﹣|1﹣ |+ .19. 已知:BE⊥CD,BE=DE,BC=DA,
 (1)、△BEC≌△DEA;
(1)、△BEC≌△DEA;
(2)、DF⊥BC.20. 如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
①画出△ABC关于y轴的对称图形△A1B1C1 , 并写出B1点的坐标;
②画出△ABC绕原点O旋转180°后得到的图形△A2B2C2 , 并写出B2点的坐标;
③在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.
21. 某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(1)、写出每天的生产成本y元(包括固定成本与原料成本)与每天的生产量x件之间的函数关系式;
(2)、如果每件产品的出厂价为1200元,那么每天至少生产多少件产品,该工厂才有盈利?22. 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点. 23. 阅读理解
23. 阅读理解∵ < < ,即2< <3.
∴1< ﹣1<2
∴ ﹣1的整数部分为1.
∴ ﹣1的小数部分为 ﹣2.
解决问题:
已知a是 ﹣3的整数部分,b是 ﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
24. 甲乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示,根据图像所提供的信息解答下列问题: (1)、乙比甲晚出发秒,乙提速前的速度是每秒cm, =;(2)、已知甲匀速走完了全程,请补全甲的图象;(3)、当x为何值时,乙追上了甲?25. 如图,已知函数y=﹣ x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
(1)、乙比甲晚出发秒,乙提速前的速度是每秒cm, =;(2)、已知甲匀速走完了全程,请补全甲的图象;(3)、当x为何值时,乙追上了甲?25. 如图,已知函数y=﹣ x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO (1)、点A的坐标为 , AC的长为;
(1)、点A的坐标为 , AC的长为;
(2)、判断∠BPQ与∠CAP的大小关系,并说明理由;
(3)、当△APQ为等腰三角形时,求点P的坐标.