2017-2018学年七年级上学期数学期末试卷
试卷更新日期:2017-12-22 类型:期末考试
一、单选题
-
1. 实数1,﹣1,0,﹣ 四个数中,最大的数是( )A、0 B、1 C、﹣1 D、﹣2. 下列判断正确的是( )A、3a2b与ba2不是同类项 B、 不是整式 C、单项式﹣x3y2的系数是﹣1 D、3x2﹣y+5xy2是二次三项式3. 如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线.其中正确的个数有( )
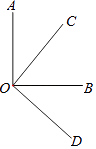 A、1个 B、2个 C、3个 D、4个4. 如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A、1个 B、2个 C、3个 D、4个4. 如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( ) A、a<1<﹣a B、a<﹣a<1 C、1<﹣a<a D、﹣a<a<15. 如果单项式 与 是同类项,那么a,b分别为( )A、2,2 B、﹣3,2 C、2,3 D、3,26. 某服装店同时以300元的价钱出售两件不同进价的衣服,其中一件赚了20%,而另一件亏损了20%.则这单买卖是( )A、不赚不亏 B、亏了 C、赚了 D、无法确定7. 小丽制作了一个对面图案均相同的正方体礼品盒(如图所示),则这个正方体礼品盒的平面展开图可能是( )
A、a<1<﹣a B、a<﹣a<1 C、1<﹣a<a D、﹣a<a<15. 如果单项式 与 是同类项,那么a,b分别为( )A、2,2 B、﹣3,2 C、2,3 D、3,26. 某服装店同时以300元的价钱出售两件不同进价的衣服,其中一件赚了20%,而另一件亏损了20%.则这单买卖是( )A、不赚不亏 B、亏了 C、赚了 D、无法确定7. 小丽制作了一个对面图案均相同的正方体礼品盒(如图所示),则这个正方体礼品盒的平面展开图可能是( )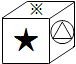 A、
A、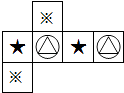 B、
B、 C、
C、 D、
D、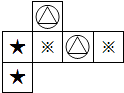 8. 已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )A、13x﹣1 B、6x2+13x﹣1 C、5x+1 D、﹣5x﹣19. 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
8. 已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )A、13x﹣1 B、6x2+13x﹣1 C、5x+1 D、﹣5x﹣19. 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )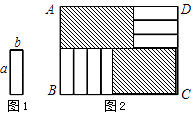 A、a=b B、a=3b C、a=2b D、a=4b
A、a=b B、a=3b C、a=2b D、a=4b二、填空题
-
10. 若有理数a、b满足|a+6|+(b﹣4)2=0,则a﹣b的值为 .11. 如果a、b互为相反数,x、y互为倒数,那么(a+b) ﹣2015xy= .12. 如图,线段AB=10cm,点C为线段AB上一点,BC=3cm,点D,E分别为AC和AB的中点,则线段DE的长为 cm.
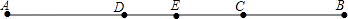 13. 用四舍五入法将3.886精确到0.01,所得到的近似数为14. 如果单项式3amb3与﹣ a2bn是同类项,那么m﹣n= .15. a与b的两倍的差可表示为.
13. 用四舍五入法将3.886精确到0.01,所得到的近似数为14. 如果单项式3amb3与﹣ a2bn是同类项,那么m﹣n= .15. a与b的两倍的差可表示为.三、计算题
-
16. 计算:
(1)、﹣20+(﹣14)﹣(﹣18)﹣13
(2)、(﹣ )×13+(﹣ )×2﹣(﹣ )×5
(3)、﹣22+5×(﹣3)﹣(﹣4)÷4(4)、﹣14﹣(1﹣0.5)× ×[2﹣(﹣3)2].17. 先化简,再求值:(4a2﹣3a)﹣(2a2+a﹣1)+(2﹣a2+4a),其中a=﹣2.四、作图题
-
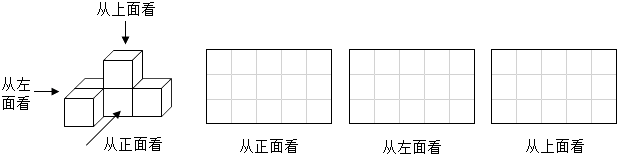
18.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的平面图形.
五、综合题
-
19. 如图,M是线段AC的中点,N是线段BC的中点.
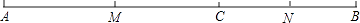
(1)、如果AC=8cm,BC=6cm,求MN的长.(2)、如果AM=5cm,CN=2cm,求线段AB的长.
20. 如图,已知OM平分∠AOC,ON平分∠BOC,∠AOB=90°,∠BOC=30°.求:
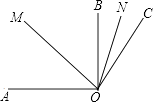 (1)、∠AOC的度数;(2)、∠MON的度数.21. 目前节能灯在城市已基本普及,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表所示:
(1)、∠AOC的度数;(2)、∠MON的度数.21. 目前节能灯在城市已基本普及,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表所示:进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、如何进货,进货款恰好为44000元?(2)、如何进货,商场销售完节能灯时恰好获利30%,此时利润为多少元?22. 如图1,点A、B分别在数轴原点O的左右两侧,且 OA+50=OB,点B对应数是90. (1)、求A点对应的数;(2)、如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离;
(1)、求A点对应的数;(2)、如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离;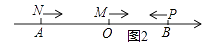 (3)、如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值.
(3)、如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值.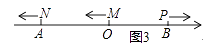
六、解答题
-
23.
如图所示,已知∠1=∠2,∠3=∠4,∠5=∠C,求证:DE//BF

-