浙江省杭州十三中教育集团2017年中考数学二模试卷
试卷更新日期:2017-12-21 类型:中考模拟
一、仔细选一选
-
1. 的倒数是( )A、﹣ B、 C、﹣ D、2. 如图,l1∥l2∥l3 , 两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知 ,则 的值为( )
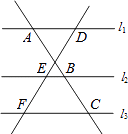 A、 B、 C、 D、3. 下列各式变形中,正确的是( )A、2x2•3x3=6x6 B、 =a C、x2﹣4=(x+4)(x﹣4) D、(a﹣b)2=(b﹣a)24. 一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体所有棱长之和为( )
A、 B、 C、 D、3. 下列各式变形中,正确的是( )A、2x2•3x3=6x6 B、 =a C、x2﹣4=(x+4)(x﹣4) D、(a﹣b)2=(b﹣a)24. 一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体所有棱长之和为( )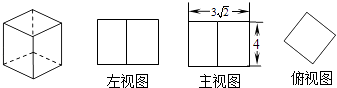 A、48 B、40 C、24 +16 D、285. 将一个半径为R,圆心角为90°的扇形围成一个圆锥的侧面(无重叠),设圆锥底面半径为r,则R与r的关系正确的是( )
A、48 B、40 C、24 +16 D、285. 将一个半径为R,圆心角为90°的扇形围成一个圆锥的侧面(无重叠),设圆锥底面半径为r,则R与r的关系正确的是( )
A、R=8r B、R=6r C、R=4r D、R=2r6. 为了缓解城市用水紧张及提倡节约用水,某市自2017年1月1日起调整居民用水价格,每立方米水费上涨25%.该市林老师家2016年12月份的水费是18元,而2017年1月份的水费是36元,且已知林老师家2017年1月份的用水量比2016年12月份的用水量多6m3 . 求该市去年的居民用水价格?设去年的居民用水价格x元/m3 , 则所列方程正确的是( )
A、 ﹣ =6 B、 ﹣ =6 C、 ﹣ =6 D、 ﹣ =67. 已知点A(﹣1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可以是( )A、 B、
B、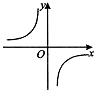 C、
C、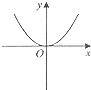 D、
D、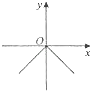 8. 如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E.若CD=5,CE=4,则⊙O的半径是( )
8. 如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E.若CD=5,CE=4,则⊙O的半径是( )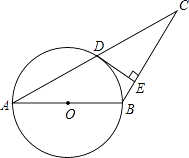 A、3 B、4 C、 D、9. 已知关于x、y的方程组 (a≥0),给出下列说法:
A、3 B、4 C、 D、9. 已知关于x、y的方程组 (a≥0),给出下列说法:①当a=1时,方程组的解也是方程x+y=2的一个解;
②当x﹣2y>8时,a> ;
③不论a取什么实数,2x+y的值始终不变;
④某直角三角形的两条直角边长分别为x+y,x﹣y,则其面积最大值为 .
以上说法正确的是( )
A、②③ B、①②④ C、③④ D、②③④二、认真填一填
-
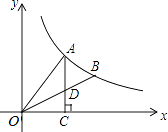
10. 在2017年政府工作报告中,总理指出今年要完成铁路建设投资8千亿元,用科学记数法表示为元.11. 若ab≠0,且2b=3a,则 的值是 .12. 有大小、形状、颜色完全相同的4个乒乓球,每个球上分别标有数字1,2,3,4,将这4个球放入不透明的袋中搅匀,从中随机连续抽取两个(不放回),则这两个球上的数字之和为偶数的概率是 .13. 已知△ABC中,AB=AC,点O为△ABC的外心,且∠BOC=90°,则∠BAC度数为 .14. 如图,A.B是双曲线y= 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为 .
 15. 如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.
15. 如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.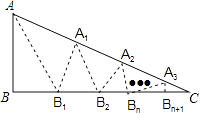 (1)、若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C (设∠B>∠C)之间的等量关系为 .
(1)、若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C (设∠B>∠C)之间的等量关系为 .
(2)、若一个三角形的最小角是4°,且该三角形的三个角均是此三角形的好角.请写出符合要求三角形的另两个角的度数 . (写出一种即可)
三、全面答一答
-
16. 计算:已知|x|= ,|y|= ,且x<y<0,求6÷(x﹣y)的值.17. 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
 (1)、只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):
(1)、只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):①点P到A,B两点的距离相等;
②点P到∠xOy的两边的距离相等.
(2)、在(1)作出点P后,写出点P的坐标.18. 在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题: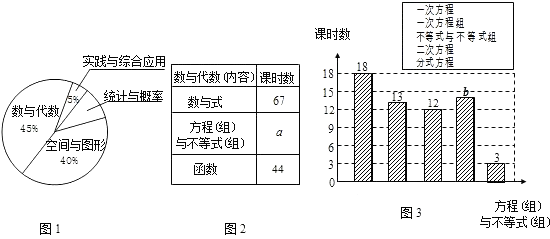 (1)、图1中“统计与概率”所在扇形的圆心角为度;
(1)、图1中“统计与概率”所在扇形的圆心角为度;
(2)、图2、3中的a= , b=;
(3)、在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
19. 如图,在▱ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD. (1)、求证:四边形ABEF是菱形;
(1)、求证:四边形ABEF是菱形;
(2)、若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
20. 如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.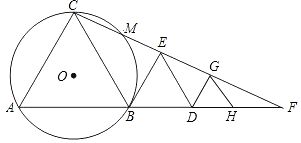 (1)、求证:AC 2=CM•CF;
(1)、求证:AC 2=CM•CF;
(2)、若CM= ,MF= ,求圆O的半径长;
(3)、设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系.
21. 已知二次函数y=(t+1)x2+2(t+2)x+ 在x=0和x=2时的函数值相等. (1)、求二次函数的解析式;
(1)、求二次函数的解析式;
(2)、若一次函数y=kx+6的图象与二次函数的图象都经过点A(﹣3,m),求m和k的值;
(3)、把二次函数的图象与x轴两个交点之间的部分记为图象G,把图象G向左平移n(n>0)个单位后得到的图象记为M,请结合图象回答:当(2)中得到的直线与图象M有公共点时,求n的取值范围.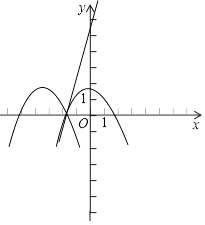 22. 如图1,O为线段AB上一点,AB=6,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
22. 如图1,O为线段AB上一点,AB=6,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.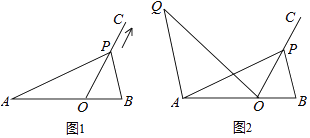 (1)、若AO=4,
(1)、若AO=4,①当t=1秒时,OP= , S△ABP=;
②当△ABP是直角三角形时,求t的值;
(2)、如图2,若点O为AB中点,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求AQ•BP的值.