内蒙古呼伦贝尔市满洲里市2017年中考数学模拟试卷
试卷更新日期：2017-12-21 类型：中考模拟
一、选择题
-
1. ﹣3的绝对值是（ ）A、﹣ B、 C、﹣3 D、32. 某自然保护区的面积为2150 000 000平方米，2150000000这个数用科学记数法表示为（ ）A、2.15×108 B、21.5×108 C、2.15×109 D、0.215×1093. 如图的几何体是由一个正方体切去一个小正方体形成的，它的主视图是（ ）
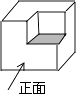A、
B、
C、
D、
4. 不等式组 的所有整数解之和是（ ）
A、﹣8 B、﹣9 C、﹣10 D、﹣125. 如图，⊙O的半径为1，A，B，C是圆周上的三点，∠BAC=36°，则劣弧BC的长是（ ）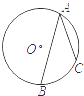
A、 B、 C、 D、6. 用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′=∠AOB的依据是（ ）
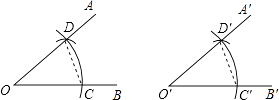A、（S、S、S） B、（S、A、S） C、（A、S、A） D、（A、A、S)7. 关于一组数据的平均数、中位数、众数，下列说法中正确的是（ ）
A、平均数一定是这组数中的某个数 B、中位数一定是这组数中的某个数 C、众数一定是这组数中的某个数 D、以上说法都不对8. 如图，已知菱形ABCD的边长为2，∠DAB=60°，则对角线BD的长是（ ）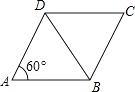
A、1 B、 C、2 D、29. 已知反比例函数y= ，下列结论中不正确的是（ ）
A、图象经过点（﹣1，﹣1） B、图象在第一、三象限 C、两个分支关于原点成中心对称 D、当x＜0时，y随着x的增大而增大10. 已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论中正确的是（ ）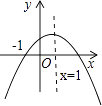
A、a＞0 B、当x＞1时，y随x的增大而增大 C、c＜0 D、3是方程ax2+bx+c=0的一个根11. 已知一个等腰三角形的两边长x，y满足方程组 ，则此等腰三角形的周长为（ ）
A、5 B、4 C、3 D、5或412. 一个寻宝游戏的寻宝通道如图1所示，通道由在同一平面内的AB，BC，CA，OA，OB，OC组成．为记录寻宝者的行进路线，在BC的中点M处放置了一台定位仪器．设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为（ ）
A、A→O→B B、B→A→C C、B→O→C D、C→B→O二、填空题
-
13. 分解因式：a2b﹣2ab+b= ．14. 为解决群众看病难的问题，一种药品连续两次降价，每盒的价格由原来的60元降至48.6元，则平均每次降价的百分率为 %．
15. 如图，是一个可以自由转动的正六边形转盘，其中三个正三角形涂有阴影，转动指针，指针落在有阴影的区域内的概率为a；如果投掷一枚硬币，正面向上的概率为b，则ab（填“＞”“＜”或“=”）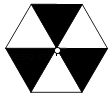
16. 如图，正方形ABCD的边长为4，E为BC上的一点，BE=1，F为AB上的一点，AF=2，P为AC上一个动点，则PF+PE的最小值为 ．
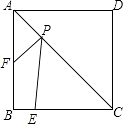17. 有这样一组数据a1 ， a2 ， a3 ， …an ， 满足以下规律：a1= ，a2= ，a3= ，…，an= （n≥2且n为正整数），则a2017的值为（结果用数字表示）
三、解答题
-
18. 计算： ﹣4cos45°+（ ）﹣1﹣| ﹣2|．
19. 某地区两个城市之间，可乘坐普通列车或高铁．已知高铁行驶线路的路程是400千米，普通列车行驶线路的路程是高铁行驶路程的1.3倍；高铁的平均速度是普通列车平均速度的2.5倍．如果乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度．
20. 如图，已知反比例函数y=﹣ 与一次函数y=kx+b的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是﹣2．求：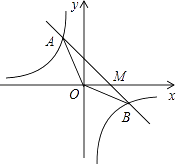
(1)、一次函数的解析式；(2)、△AOB的面积．21. 小丽学完统计知识后，随机调查了她所在辖区若干名居民的年龄，将调查数据绘制成如下扇形和条形统计图：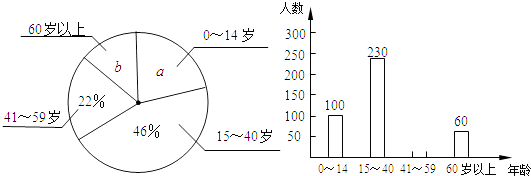
请根据以上不完整的统计图提供的信息，解答下列问题：
(1)、小丽同学共调查了名居民的年龄，扇形统计图中a= ， b= ， 中位数在年龄段内；(2)、补全条形统计图；(3)、若该辖区年龄在0～14岁的居民约有3500人，请估计年龄在15～59岁的居民的人数．
22. 某大桥采用低塔斜拉桥桥型（如甲图），图乙是从图甲引申出的平面图，假设你站在桥上测得拉索AB与水平桥面的夹角是30°，拉索CD与水平桥面的夹角是60°，两拉索顶端的距离BC为2米，两拉索底端距离AD为20米，请求出立柱BH的长．（结果精确到0.1米， ≈1.732）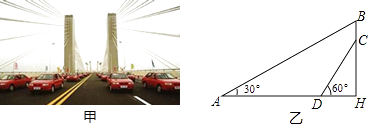
23. 有3张不透明的卡片，除正面写有不同的数字外，其它均相同．将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片标有的数字记作一次函数表达式中的k，第二次从余下的两张卡片中再随机抽取一张，上面标有的数字记作一次函数表达式中的b．
(1)、写出k为负数的概率；
(2)、求一次函数y=kx+b的图象经过二、三、四象限的概率．（用树状图或列表法求解）
24. 在正方形ABCD中，过点A引射线AH，交边CD于点H（点H与点D不重合），通过翻折，使点B落在射线AH上的点G处，折痕AE交BC于点E，延长EG交CD于点F．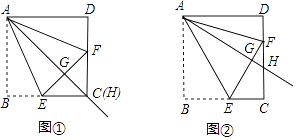
(1)、如图①，当点H与点C重合时，易证得FG=FD（不要求证明）；如图②，当点H为边CD上任意一点时，求证：FG=FD．
(2)、【应用】在图②中，已知AB=5，BE=3，则FD= ， △EFC的面积为 ． （直接写结果）
25. 如图，在△ABC中，AB=AC，点D在BC上，BD=DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．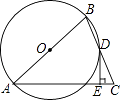
(1)、求证：AB是⊙O的直径；
(2)、判断DE与⊙O的位置关系，并加以证明；
(3)、若⊙O的半径为3，∠BAC=60°，求DE的长．26. 如图（1），抛物线 y=﹣ x2平移后过点A（8，0）和原点，顶点为B，对称轴与x轴相交于点C，与原抛物线相交于点D．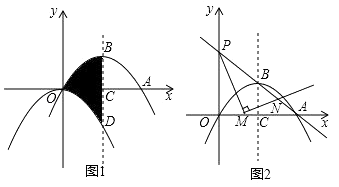
(1)、求平移后抛物线的解析式及点D的坐标；(2)、直接写出阴影部分的面积 S阴影；(3)、如图（2），直线AB与y轴相交于点P，点M为线段OA上一动点（点M不与点A，O重合 ），∠PMN为直角，MN与AP相交于点N，设OM=t，试探究：t为何值时，△MAN为等腰三角形？