黑龙江省哈工大附中2017年中考数学模拟试卷(5月份)
试卷更新日期:2017-12-21 类型:中考模拟
一、选择题
-
1. 我市4月份某天的最高气温是15℃,最低气温是﹣2℃,那么这天的温差(最高气温减最低气温)是( )A、﹣13℃ B、13℃ C、﹣17℃ D、17℃2. 下列计算正确的是( )
A、x+x2=x3 B、2x+3x=5x2 C、(x2)3=x6 D、x6÷x3=x23. 下列LOGO标志中,是中心对称图形,但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 已知反比例函数y= 的图象位于第一、第三象限,则k的取值范围是( )A、k>2 B、k≥2 C、k≤2 D、k<25. 如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )
4. 已知反比例函数y= 的图象位于第一、第三象限,则k的取值范围是( )A、k>2 B、k≥2 C、k≤2 D、k<25. 如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )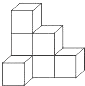 A、
A、 B、
B、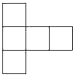 C、
C、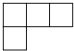 D、
D、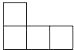 6. 如图,某河堤迎水坡AB的坡比i=1: ,堤高BC=5m,则坡面AB的长是( )
6. 如图,某河堤迎水坡AB的坡比i=1: ,堤高BC=5m,则坡面AB的长是( ) A、5 m B、10m C、15 m D、20 m7. 如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
A、5 m B、10m C、15 m D、20 m7. 如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )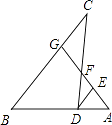 A、 = B、 = C、 = D、 =8. 某初中决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是( )
A、 = B、 = C、 = D、 =8. 某初中决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.若CD=3,BC+AB=16,则△ABC的面积为( ) A、16 B、18 C、24 D、3210. 甲乙两名大学生去距学校36千米的某乡镇进行社会调查,他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车继续前往乡镇,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图,则下列结论:①电动车的速度为0.9千米/分;②甲步行所用的时间为45分;③甲步行的速度为0.15千米/分;④乙返回学校时,甲与学校相距20千米.其中正确的个数是( )
A、16 B、18 C、24 D、3210. 甲乙两名大学生去距学校36千米的某乡镇进行社会调查,他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车继续前往乡镇,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图,则下列结论:①电动车的速度为0.9千米/分;②甲步行所用的时间为45分;③甲步行的速度为0.15千米/分;④乙返回学校时,甲与学校相距20千米.其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 将数据65200用科学记数法表示为 .12. 函数y= 中,自变量x的取值范围是 .
13. 计算: ﹣3 = .14. 因式分解:4ax2+16axy+16ay2= .15. 不等式组 的最大整数解是 .16. 扇形的弧长为12π,圆心角是120°,则扇形的半径长为 .
17. 某超市今年一月份的营业额为60万元.三月份的营业额为135万元.若每月营业额的平均增长,则二月份的营业额是万元.
18. Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(如图).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= . 19. 如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC= .
19. 如图,直线L与⊙O相切于点D,半径R=5,过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点,BD=12,则tan∠ABC= . 20. 已知点D与点A(4,0),B(0,3),C(a,﹣a)是一平行四边形的四个顶点,则CD长的最小值为 .
20. 已知点D与点A(4,0),B(0,3),C(a,﹣a)是一平行四边形的四个顶点,则CD长的最小值为 .三、解答题
-
21. 先化简,再求代数式的值:( ﹣x+2)÷ ,其中x=3tan30°﹣(3.14﹣π)0 .22. 已知,如图平面直角坐标系内,O为坐标原点,A(﹣1,3),B(﹣5,﹣1),连接AB,

①请画出将线段AB绕点O顺时针旋转90°得到的线段CD(C为A旋转后的对应点),并直接写出C、D两点的坐标;
②连接BC、BD,构成△BCD,用一条线段将△BCD分割成两部分后,再拼成一个相邻两边长分别为 和4 的中心对称图形.
23. 考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中信息解答下列问题: (1)、这次抽样调查中,一共抽查了多少名学生?
(1)、这次抽样调查中,一共抽查了多少名学生?
(2)、请补全条形统计图;
(3)、请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)、根据调查结果,估计该校九年级500名学生中采用“听音乐”来减压方式的人数.
24. 如图,在△ABC中,CD是AB上的高,将△BCD沿直线CB翻折得到△BCE,使D落到E处,且∠ACE=90°. (1)、求证:△ABC为等腰三角形;(2)、若BD=2,tan∠A= ,求AC的长.25. 某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)、求证:△ABC为等腰三角形;(2)、若BD=2,tan∠A= ,求AC的长.25. 某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)、求购买一个甲种足球、一个乙种足球各需多少元?(2)、为响应“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
26. 如图,△ABC内接于⊙O,AD⊥BC于点D,半径ON⊥BC于点G,连接OB. (1)、如图1,求证:∠ACB﹣∠OBG=∠BAD;(2)、如图2,弦BH交AC于点E,交AD于点F,AH=2OG,求证:AF=AH;(3)、如图3,在(2)的条件下,连接FG、CH,∠BFG=∠ACH,OG= ,CH=3,求线段CD的长.27. 在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4a与x轴交于点A、点B(点A在点B的左侧),与y轴交于点C,点P在第二象限的抛物线上,PD⊥y轴于点D,连接PC交x轴于点E,设PD的长为n,OE的长为m.
(1)、如图1,求证:∠ACB﹣∠OBG=∠BAD;(2)、如图2,弦BH交AC于点E,交AD于点F,AH=2OG,求证:AF=AH;(3)、如图3,在(2)的条件下,连接FG、CH,∠BFG=∠ACH,OG= ,CH=3,求线段CD的长.27. 在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4a与x轴交于点A、点B(点A在点B的左侧),与y轴交于点C,点P在第二象限的抛物线上,PD⊥y轴于点D,连接PC交x轴于点E,设PD的长为n,OE的长为m. (1)、如图1,求m与n的函数关系式;
(1)、如图1,求m与n的函数关系式;
(2)、如图1,作EQ⊥x轴,EQ交抛物线于点Q,连接CQ并延长交x轴于点F,连接PF,求证:PF∥OC;(3)、如图2,在(2)的条件下,连接AC、PB、FD,PB交FD于点K,当点E为PC的中点,∠FCA+∠PKF=3∠PBF时,求点P的坐标.