山东省临沂市河东区2017-2018学年九年级上学期数学开学考试试卷
试卷更新日期:2017-12-20 类型:开学考试
一、选择题
-
1. 一元二次方程2x2+3x+1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定2. 将抛物线y=x2向右平移2个单位,再向上平移3个单位后,抛物线的解析式为( )A、y=(x+2)2+3 B、y=(x﹣2)2+3 C、y=(x+2)2﹣3 D、y=(x﹣2)2﹣33. 一次函数y=2x﹣3的图象不经过的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若五个正整数的中位数是3,且唯一的众数是7,则这五个数的平均数是( )
A、4 B、5 C、6 D、85. 已知菱形的两条对角线长分别是6cm和8cm,则菱形的边长是( )
A、5cm B、7cm C、10cm D、12cm6. 如图,矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,BD=8,则AB的长为( ) A、4 B、 C、3 D、57. 已知P1(﹣1,y1),P2(2,y2)是一次函数y=﹣x+1图象上的两个点,则y1 , y2的大小关系是( )
A、4 B、 C、3 D、57. 已知P1(﹣1,y1),P2(2,y2)是一次函数y=﹣x+1图象上的两个点,则y1 , y2的大小关系是( )
A、y1=y2 B、y1<y2 C、y1>y2 D、不能确定8. 如图,四边形OABC是正方形,已知O(0,0),A( ,0),则OB的长为( ) A、 B、2 C、2 D、49. 下列四边形:①菱形;②正方形;③矩形;④平行四边形.对角线一定相等的是( )
A、 B、2 C、2 D、49. 下列四边形:①菱形;②正方形;③矩形;④平行四边形.对角线一定相等的是( )
A、①② B、②③ C、①②③ D、①②③④10. 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( ) A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.511. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )A、
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.511. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )A、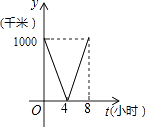 B、
B、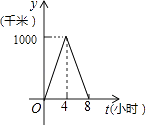 C、
C、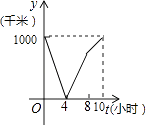 D、
D、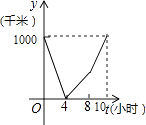
二、填空题
-
12. 若x=1是一元二次方程x2+2x+m=0的一个根,则m的值为13. 方程3(x﹣5)2=2(x﹣5)的根是 .
14. 二次函数y=x2﹣4x﹣3的顶点坐标是 .15. 如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=cm. 16. 如图,一次函数y=kx+b与y=﹣x+5的图象的交点坐标为(2,3),则关于x的不等式﹣x+5>kx+b的解集为 .
16. 如图,一次函数y=kx+b与y=﹣x+5的图象的交点坐标为(2,3),则关于x的不等式﹣x+5>kx+b的解集为 . 17. 正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于F,则EF的长为 .
17. 正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于F,则EF的长为 .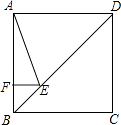
三、解答题
-
18. 向阳村2014年的人均收入为12000元,2016年的人均收入为14520元,求人均收入的年平均增长率.
19. 如图,BD是▱ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.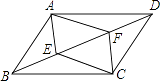 20. 已知二次函数y=﹣x2+2x+m.
20. 已知二次函数y=﹣x2+2x+m. (1)、如果二次函数的图象与x轴有两个交点,求m的取值范围;
(1)、如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)、如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
21. 如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.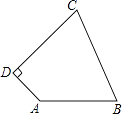 22. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
22. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD. (1)、求证:四边形AODE是矩形;
(1)、求证:四边形AODE是矩形;
(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.
23. 如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12. (1)、求点E的坐标:(2)、求△OPE的周长.24. 某乡A,B两村盛产大蒜,A村有大蒜200吨,B村有大蒜300吨,现将这些大蒜运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的大蒜为x吨,A,B两村运大蒜往两仓库的运输费用分别为yA元,yB元.
(1)、求点E的坐标:(2)、求△OPE的周长.24. 某乡A,B两村盛产大蒜,A村有大蒜200吨,B村有大蒜300吨,现将这些大蒜运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的大蒜为x吨,A,B两村运大蒜往两仓库的运输费用分别为yA元,yB元.
(1)、请填写下表,并求出yA , yB与x之间的函数关系式;C
D
总计
A
x吨
200吨
B
300吨
总计
240吨
260吨
500吨
(2)、当x为何值时,A村的运费较少?
(3)、请问怎样调运,才能使两村的运费之和最小?求出最小值.