江苏省南通市启东市2017-2018学年九年级上学期数学开学考试试卷

试卷更新日期：2017-12-20 类型：开学考试

进入出卷网下载

一、选择题

1. 在下列平面图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各组数中，以a，b，c为边的三角形不是直角三角形的是（）

A、a=1.5，b=2，c=3 B、a=7，b=24，c=25 C、a=6，b=8，c=10 D、a=3，b=4，c=5

查看试题解析
3. 某小区2014年屋顶绿化面积为2000平方米，计划2016年屋顶绿化面积要达到2880平方米．若设屋顶绿化面积的年平均增长率为x，则依题意所列方程正确的是（　　）

A、2000（1+x）²=2880 B、2000（1﹣x）²=2880 C、2000（1+2x）=2880 D、2000x²=2880

查看试题解析
4. 在下列函数关系式：①y=x；②y=2x+1；③y=x²﹣x+1；④y= $\frac{1}{x}$ ．其中，一次函数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若m、n是一元二次方程x²﹣5x﹣2=0的两个实数根，则m+n﹣mn的值是（）

A、﹣7 B、7 C、3 D、﹣3

查看试题解析
6. 甲和乙一起练习射击，第一轮10枪打完后两人的成绩如图所示．设他们这10次射击成绩的方差为S_甲²、S_乙² ，下列关系正确的是（）

A、S_甲²＜S_乙² B、S_甲²＞S_乙² C、S_甲²=S_乙² D、无法确定

查看试题解析
7. 如图，在同一平面直角坐标系中，表示一次函数y=mx+n与正比例函数y=mnx（m，n是常数，且mn≠0）图象的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，在△ABC中，AB=AC=5，BC=8，D是线段BC上的动点（不含端点B、C）．若线段AD长为正整数，则点D的个数共有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
9. 如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为（）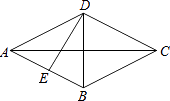

A、2.4cm B、4.8cm C、5cm D、9.6cm

查看试题解析
10. 如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（）

A、 $\frac{8 \sqrt{3}}{5}$ B、2 $\sqrt{2}$ C、 $\frac{14}{5}$ D、10﹣5 $\sqrt{2}$

查看试题解析

二、填空题

11. 一组数据5，﹣2，3，x，3，﹣2，若每个数据都是这组数据的众数，则这组数据的平均数是．

查看试题解析
12. 已知点（﹣4，y₁）、（2，y₂）都在直线y=﹣0.5x+2上，则y₁与y₂的大小关系是．

查看试题解析
13. 现定义运算“★”，对于任意实数a、b，都有a★b=a²﹣3a+b，如：3★5=3²﹣3×3+5，若x★2=6，则实数x的值是．

查看试题解析
14. 如图，将Rt△ABC绕直角顶点A顺时针旋转90°，得到△AB′C′，连结BB′，若∠1=20°，则∠C的度数是．

查看试题解析
15. 如图，把一张矩形的纸沿对角线BD折叠，若AD=8，CE=3，则DE= ．

查看试题解析
16. 如图，正方形ABCD的对角线长为8 $\sqrt{2}$ ，E为AB上一点，若EF⊥AC于F，EG⊥BD于G，则EF+EG= ．

查看试题解析
17. 某种植物的主干长出若干数目的支干，每个支干又长出同样多数目的小分支，主干、支干、小分支一共是91个，则每个支干长出的小分支数目为

查看试题解析
18. 平面直角坐标系中有两点M（a，b），N（c，d），规定（a，b）⊕（c，d）=（a+c，b+d），则称点Q（a+c，b+d）为M，N的“和点”．若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形，则称这个四边形为“和点四边形”，现有点A（2，5），B（﹣1，3），若以O，A，B，C四点为顶点的四边形是“和点四边形”，则点C的坐标是．

查看试题解析

三、解答题

19. 用合适的方法解下列方程

(1)、x²﹣6x+5=0

(2)、3（x﹣2）=x（x﹣2）

查看试题解析
20. 城东中学七年级举行跳绳比赛，要求与每班选出5名学生参加，在规定时间每人跳绳不低于150次为优秀，冠、亚军在甲、乙两班中产生，如表是这两个班的5名学生的比赛数据（单位：次）

1号
2号
3号
4号
5号
平均次数
方差
甲班
150
148
160
139
153
150
46.8
乙班
139
150
145
169
147
a
103.2
根据以上信息，解答下列问题：

(1)、写出表中a的值和甲、乙两班的优秀率；

(2)、写出两班比赛数据的中位数；

(3)、你认为冠军奖应发给那个班？简要说明理由．

查看试题解析
21. 如图，在平面直角坐标系xOy中，△ABC三个顶点的坐标分别为A（﹣2，﹣1），B（﹣4，1），C（﹣3，3）．△ABC关于原点O对称的图形是△A₁B₁C₁ ．

(1)、画出△A₁B₁C₁；

(2)、BC与B₁C₁的位置关系是， AA₁的长为；

(3)、若点P（a，b）是△ABC 一边上的任意一点，则点P经过上述变换后的对应点P₁的坐标可表示为．

查看试题解析
22. 关于x的方程x²﹣x+a=0有实根．

(1)、求a的取值范围；

(2)、设x₁、x₂是方程的两个实数根，且满足（x₁+1）（x₂+1）=﹣1，求实数a的值．

查看试题解析
23. 已知直线y=kx+b经过点A（5，0），B（1，4）．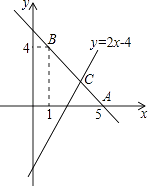

(1)、求直线AB的解析式；

(2)、若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；

(3)、根据图象，写出关于x的不等式2x﹣4＞kx+b的解集．

查看试题解析
24. 如图，△ACB和△ECD都是等腰直角三角形，△ACB的顶点A在△ECD的斜边DE上，
求证：AE²+AD²=2AC² ．

查看试题解析
25. 如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t（s）．

(1)、当t为何值时，PQ∥CD？

(2)、当t为何值时，PQ=CD？

查看试题解析
26. A市和B市库存某种机器分别为12台和6台，现决定支援给C市10台和D市8台，已知从A市调运一台机器到C市和D市的运费分别为400元和800元，从B市调运一台机器到C市和D市的运费分别为300元和500元．

(1)、设B市运往C市的机器x台，求总运费W（元）与x的函数式．

(2)、若要求总运费不超过9000元，问：共有几种调运方案．

(3)、请选择最佳调运方案，使总运费最少，并求出最少总运费．

查看试题解析
27. 阅读材料：
我们经常通过认识一个事物的局部或其特殊类型，来逐步认识这个事物；比如我们通过学习特殊的四边形，即平行四边形（继续学习它们的特殊类型如矩形、菱形等）来逐步认识四边形；

我们对课本里特殊四边形的学习，一般先学习图形的定义，再探索发现其性质和判定方法，然后通过解决简单的问题巩固所学知识；
请解决以下问题：
如图，我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”；

(1)、写出筝形的两个性质（定义除外）；

(2)、写出筝形的两个判定方法（定义除外），并选出一个进行证明．

查看试题解析
28. 已知O是坐标原点，点A的坐标是（5，0），点B是y轴正半轴上一动点，以OB、OA为边作矩形OBCA，点E、H分别在边BC和边OA上，将△BOE沿着OE对折，使点B落在OC上的F点处，将△ACH沿着CH对折，使点A落在OC上的G点处．

(1)、如图1，求证：四边形OECH是平行四边形；

(2)、如图2，当点B运动到使得点F、G重合时，求点B的坐标，并判断四边形OECH是什么四边形？说明理由；

(3)、当点B运动到使得点F，G将对角线OC三等分时，如图3，如图4，分别求点B的坐标．

查看试题解析

	1号	2号	3号	4号	5号	平均次数	方差
甲班	150	148	160	139	153	150	46.8
乙班	139	150	145	169	147	a	103.2