黑龙江省哈尔滨156中2017-2018学年九年级上学期数学开学考试试卷（五四学制）

试卷更新日期：2017-12-20 类型：开学考试

进入出卷网下载

一、选择题

1. 下列各数中，最小的数是（）

A、0 B、﹣ $\frac{1}{3}$ C、 $\sqrt{3}$ D、﹣3

查看试题解析
2. 下列运算正确的是（）

A、2x+3y=5xy B、5m²•m³=5m⁵ C、（a﹣b）²=a²﹣b² D、m²•m³=m⁶

查看试题解析
3. 由二次函数y=2（x﹣3）²+1，可知（）

A、其图象的开口向下 B、其图象的对称轴为直线x=﹣3 C、其最小值为1 D、当x＜3时，y随x的增大而增大

查看试题解析
4. 若x的一元二次方程kx²﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（）

A、k≤﹣1且k≠0 B、k＜﹣1且k≠0 C、k≥﹣1且k≠0 D、k＞﹣1且k≠0

查看试题解析
5. 施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则根据题意所列方程正确的是（）

A、 $\frac{2000}{x}$ ﹣ $\frac{2000}{x + 50}$ =2 B、 $\frac{2000}{x + 50}$ ﹣ $\frac{2000}{x}$ =2 C、 $\frac{2000}{x}$ ﹣ $\frac{2000}{x - 50}$ =2 D、 $\frac{2000}{x - 50}$ ﹣ $\frac{2000}{x}$ =2

查看试题解析
6.
如图所示，△ABC中若DE∥BC，EF∥AB，则下列比例式正确的是（　　）

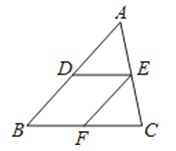A、 $\frac{A D}{D B}$ = $\frac{D E}{B C}$ B、 $\frac{B F}{B C}$ = $\frac{E F}{A D}$ C、 $\frac{A E}{E C}$ = $\frac{B F}{F C}$ D、 $\frac{E F}{A B}$ = $\frac{D E}{B C}$

查看试题解析
7. 如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（）

A、8 B、10 C、12 D、14

查看试题解析
8. 如图，矩形ABCD中，AD=2，AB=3，过点A，C作相距为2的平行线段AE，CF，分别交CD，AB于点E，F，则DE的长是（）

A、 $\sqrt{5}$ B、 $\frac{13}{6}$ C、1 D、 $\frac{5}{6}$

查看试题解析
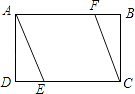9. 如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论错误的是（）

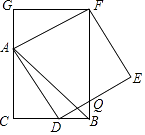A、AC=FG B、S_△_FAB：S_四边形_CBFG=1：2 C、AD²=FQ•AC D、∠ADC=∠ABF

查看试题解析
10. 如图，抛物线y=﹣x²+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D．下列四个命题：①当x＞0时，y＞0； ②若a=﹣1，则b=3；③抛物线上有两点P（x₁ ， y₁）和Q（x₂ ， y₂），若x₁＜1＜x₂ ，且x₁+x₂＞2，则y₁＞y₂；④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为6 $\sqrt{2}$ ．其中正确的命题有（）个．

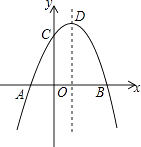A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 用科学记数法表示53700000是．

查看试题解析
12. 若 $\sqrt{1 - 3 x}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
13. 分解因式：4ax²﹣ay²= ．

查看试题解析
14. 不等式组 ${\begin{matrix} 2 + x > 0 \\ 2 x - 6 \leq 0 \end{matrix}$ 的解集是．

查看试题解析
15. 如图，P为平行四边形ABCD边AD上一点，E、F分别为PB、PC的中点，△PEF、△PDC、△PAB的面积分别为S、S₁、S₂ ，若S=2，则S₁+S₂= ．

查看试题解析
16. 如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．∠BAD=60°，AC平分∠BAD，AC=2，BN的长为．

查看试题解析
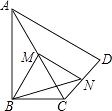17. 某公司2012年的利润为160万元，到了2014年的利润达到了250万元．设平均每年利润增长的百分率为x，则可列方程为．

查看试题解析
18. 如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是 cm．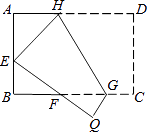

查看试题解析
19. △ABD中，AB=BD，点C在直线BD上，BD=3CD，cos∠CAD= $\frac{5}{6}$ ，AD=6，则AC= ．

查看试题解析
20. 已知图，正方形ABCD，M是BC延长线上一点，过B作BE⊥DM于点E，交DC于点F，过F作FG∥BC交BD于点G，连接GM，若S_△_EFD= 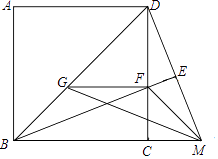$\frac{1}{8}$ DF² ， AB=4 $\sqrt{2}$ ，则GM= ．

查看试题解析

三、解答题

21. 先化简，再求代数式 $\frac{x + 1}{x}$ ÷（x﹣ $\frac{x^{2} + 1}{2 x}$ ）的值，其中x=2sin60°+tan45°．

查看试题解析
22. 如图，每个小正方形的边长都是1的方格纸中，有线段AB和线段CD，点A、B、C、D的端点都在小正方形的顶点上．

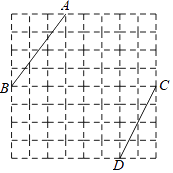(1)、①在方格纸中画出一个以线段AB为一边的菱形ABEF，所画的菱形的各顶点必须在小正方形的顶点上，并且其面积为20．
②在方格纸中以CD为底边画出等腰三角形CDK，点K在小正方形的顶点上，且△CDK的面积为5．

(2)、在（1）的条件下，连接BK，请直接写出线段BK的长．

查看试题解析
23. 如图，在▱ABCD中，点E在边BC上，点F在边AD的延长线上，且DF=BE，EF与CD交于点G．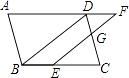

(1)、求证：BD∥EF；

(2)、若 $\frac{D G}{G C}$ = $\frac{2}{3}$ ，BE=4，求EC的长．

查看试题解析
24. 如图，防洪大堤的横截面是梯形ABCD，其中AD∥BC，α=60°，汛期来临前对其进行了加固，改造后的背水面坡角β=45°．若原坡长AB=20m，求改造后的坡长AE．（结果保留根号）

查看试题解析
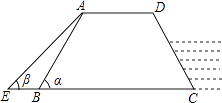25. 某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边的长为x米．

(1)、若苗圃园的面积为72平方米，求x；

(2)、若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；

(3)、当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围．

查看试题解析
26. 如图，点O为正方形ABCD对角线的交点，点E，F分别在DA和CD的延长线上，且AE=DF，连接BE，AF，延长FA交BE于G．

(1)、试判断FG与BE的位置关系，并证明你的结论；

(2)、连接OG，求∠OGF的度数；

(3)、若AE= $\sqrt{5}$ ，tan∠ABG= $\frac{1}{2}$ ，求OG的长．

查看试题解析
27. 如图，平面直角坐标系中，O为坐标原点，抛物线y=﹣ $\frac{3}{16}$ ax²+ $\frac{5}{8}$ ax+3a（a≠0）与x轴交于A和点B（A在左，B在右），与y轴的正半轴交于点C，且OB=OC．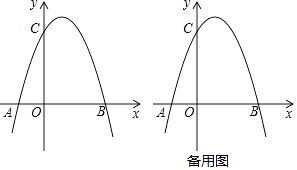

(1)、求抛物线的解析式；

(2)、若D为OB中点，E为CO中点，动点F在y轴的负半轴上，G在线段FD的延长线上，连接GE、ED，若D恰为FG中点，且S_△_GDE= $\frac{27}{2}$ ，求点F的坐标；

(3)、在（2）的条件下，动点P在线段OB上，动点Q在OC的延长线上，且BP=CQ．连接PQ与BC交于点M，连接GM并延长，GM的延长线交抛物线于点N，连接QN、GP和GB，若角满足∠QPG﹣∠NQP=∠NQO﹣∠PGB时，求NP的长．

查看试题解析