江西省赣州市十四县(市)2017-2018学年高三上学期理数期中考试试卷
试卷更新日期:2017-12-18 类型:期中考试
一、选择题
-
1. A={x|y=lg(x2+3x﹣4)}, ,则A∩B=( )A、(0,2] B、(1,2] C、∅ D、(﹣4,0)2. 对于实数a,b,c,下列命题正确的是( )A、若a>b,则ac2>bc2 B、若a<b<0,则a2>ab>b2 C、若a<b<0,则 D、若a<b<0,则3. 下列四种说法正确的是( )
①函数f(x)的定义域是R,则“∀x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的充要条件;
②命题“ ”的否定是“ ”;
③命题“若x=2,则x2﹣3x+2=0”的逆否命题是真命题;
④p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数,则p∧q为真命题.
A、①②③④ B、②③ C、③④ D、③4. 设x=0.20.3 , y=0.30.2 , z=0.30.3 , 则x,y,z的大小关系为( )A、x<z<y B、y<x<z C、y<z<x D、z<y<x5. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织九匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布?”若一个月按31天算,记该女子一个月中的第n天所织布的尺数为an , 则 的值为( )A、 B、 C、 D、6. 若变量x,y满足|x|﹣ln =0,则y关于x的函数图象大致是( )A、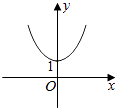 B、
B、 C、
C、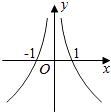 D、
D、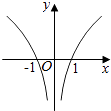 7. 方程 有解,则a的最小值为( )A、2 B、 C、1 D、8. 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其导函数f′(x)的部分图象如图所示,则函数f(x)的解析式为( )
7. 方程 有解,则a的最小值为( )A、2 B、 C、1 D、8. 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其导函数f′(x)的部分图象如图所示,则函数f(x)的解析式为( )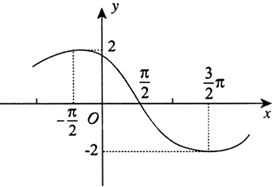 A、f(x)=4sin( x+ π) B、f(x)=4sin( x+ ) C、f(x)=4sin( x+ ) D、f(x)=4sin( x+ )9. 设a∈R,若函数y=x+alnx在区间 上有极值点,则a的取值范围为( )A、 B、 C、 D、10. 已知函数f(x)= 的值域是[0,2],则实数a的取值范围是( )A、(0,1] B、[1, ] C、[1,2] D、[ ,2]11. 若函数 ,则关于m的不等式 的解集为( )A、 B、(0,2) C、 D、12. 已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:
A、f(x)=4sin( x+ π) B、f(x)=4sin( x+ ) C、f(x)=4sin( x+ ) D、f(x)=4sin( x+ )9. 设a∈R,若函数y=x+alnx在区间 上有极值点,则a的取值范围为( )A、 B、 C、 D、10. 已知函数f(x)= 的值域是[0,2],则实数a的取值范围是( )A、(0,1] B、[1, ] C、[1,2] D、[ ,2]11. 若函数 ,则关于m的不等式 的解集为( )A、 B、(0,2) C、 D、12. 已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:①当x>0时,f(x)=﹣e﹣x(x﹣1);
②函数f(x)有2个零点;
③f(x)<0的解集为(﹣∞,﹣1)∪(0,1),
④∀x1 , x2∈R,都有|f(x1)﹣f(x2)|<2.其中正确命题的个数是( )
A、4 B、3 C、2 D、1二、填空题
-
13. 已知向量 夹角为45°,且 ,则 = .14. (x2+ )dx= .15. 在△ABC中,a,b,c为∠A,∠B,∠C的对边,a,b,c成等比数列, ,则 = .16. 已知定义在R上的函数 ,若函数g(x)=f(x)﹣a(x+1)恰有2个零点,则实数a的取值范围是 .
三、解答题
-
17. 已知正项等比数列{an}满足a1 , 2a2 , a3+6成等差数列,且a42=9a1a5 .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ,求数列{bn}的前n项和Tn .
18. 在△ABC中,A、B、C的对边分别为a,b,c,已知A≠ , 且3sinAcosB+bsin2A=3sinC.(I)求a的值;
(Ⅱ)若A= , 求△ABC周长的最大值.
19. 已知命题p:函数f(x)=x3+ax2+x在R上是增函数;命题q:若函数g(x)=ex﹣x+a在区间[0,+∞)没有零点.(1)、如果命题p为真命题,求实数a的取值范围;(2)、命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.20. 已知向量 =( sinωx,1), =(cosωx,cos2ωx+1),设函数f(x)= .(1)、若函数f(x)的图象关于直线x= 对称,且ω∈[0,3]时,求函数f(x)的单调增区间;(2)、在(1)的条件下,当 时,函数f(x)有且只有一个零点,求实数b的取值范围.
21. 某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?
 22. 已知函数f(x)=lnx﹣ ,g(x)=ax+b.(1)、若函数h(x)=f(x)﹣g(x)在(0,+∞)上单调递增,求实数a的取值范围;(2)、若直线g(x)=ax+b是函数f(x)=lnx﹣ 图象的切线,求a+b的最小值;(3)、当b=0时,若f(x)与g(x)的图象有两个交点A(x1 , y1),B(x2 , y2),求证:x1x2>2e2 .
22. 已知函数f(x)=lnx﹣ ,g(x)=ax+b.(1)、若函数h(x)=f(x)﹣g(x)在(0,+∞)上单调递增,求实数a的取值范围;(2)、若直线g(x)=ax+b是函数f(x)=lnx﹣ 图象的切线,求a+b的最小值;(3)、当b=0时,若f(x)与g(x)的图象有两个交点A(x1 , y1),B(x2 , y2),求证:x1x2>2e2 .(取e为2.8,取ln2为0.7,取 为1.4)