北京市朝阳区2017-2018学年高三上学期理数期中考试试卷

试卷更新日期：2017-12-18 类型：期中考试

进入出卷网下载

一、选择题

1. 已知集合A={x|x＞1}，B={x|log₂x＞1}，则A∩B=（）

A、{x|x＞1} B、{x|1＜x＜2} C、{x|x＞2} D、{x|x＞0}

查看试题解析
2. 已知实数x，y满足条件 ${\begin{matrix} x \geq 2 \\ y \geq 2 \\ x + y \leq 6 \end{matrix}$ 则x+2y的最大值为（）

A、12 B、10 C、8 D、6

查看试题解析
3. 要想得到函数 $y = s i n (2 x - \frac{π}{3})$ 的图象，只需将函数y=sinx的图象上所有的点（）

A、先向右平移 $\frac{π}{3}$ 个单位长度，再将横坐标伸长为原来的2倍，纵坐标不变 B、先向右平移 $\frac{π}{6}$ 个单位长度，横坐标缩短为原来的 $\frac{1}{2}$ 倍，纵坐标不变 C、横坐标缩短为原来的 $\frac{1}{2}$ 倍，纵坐标不变，再向右平移 $\frac{π}{6}$ 个单位长度 D、横坐标变伸长原来的2倍，纵坐标不变，再向右平移 $\frac{π}{3}$ 个单位长度

查看试题解析
4. 已知非零平面向量 $\vec{a}$ ， $\vec{b}$ ，则“| $\vec{a} + \vec{b}$ |=| $\vec{a}$ |+| $\vec{b}$ |”是“存在非零实数λ，使 $\vec{b}$ =λ $\vec{a}$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 已知S_n是等差数列{a_n}（n∈N^*）的前n项和，且S₅＞S₆＞S₄ ，以下有四个命题：
①数列{a_n}中的最大项为S_10；②数列{a_n}的公差d＜0；
③S₁₀＞0；④S₁₁＜0；
其中正确的序号是（）

A、②③ B、②③④ C、②④ D、①③④

查看试题解析
6. 如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，E是CD的中点DC=1，AB=2，则 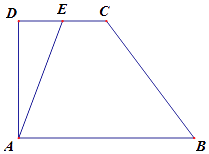$\vec{E A} \cdot \vec{A B}$ =（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、1 D、﹣1

查看试题解析
7. 袋子里有编号为2，3，4，5，6的五个球，某位教师从袋中任取两个不同的球．教师把所取两球编号的和只告诉甲，其乘积只告诉乙，再让甲、乙分别推断这两个球的编号．
甲说：“我无法确定．”
乙说：“我也无法确定．”
甲听完乙的回答以后，甲说：“我现在可以确定两个球的编号了．”
根据以上信息，你可以推断出抽取的两球中（）

A、一定有3号球 B、一定没有3号球 C、可能有5号球 D、可能有6号球

查看试题解析
8. 已知函数f（x）=sin（cosx）﹣x与函数g（x）=cos（sinx）﹣x在区间 $(0 ， \frac{π}{2})$ 内都为减函数，设 $x_{1} ， x_{2} ， x_{3} \in (0 ， \frac{π}{2})$ ，且cosx₁=x₁ ， sin（cosx₂）=x₂ ， cos（sinx₃）=x₃ ，则x₁ ， x₂ ， x₃的大小关系是（）

A、x₁＜x₂＜x₃ B、x₃＜x₁＜x₂ C、x₂＜x₁＜x₃ D、x₂＜x₃＜x₁

查看试题解析

二、填空题

9. 执行如图所示的程序框图，则输出i的值为．

查看试题解析
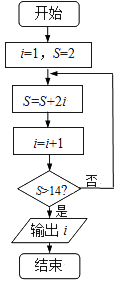10. 已知x＞1，且x﹣y=1，则 $x + \frac{1}{y}$ 的最小值是．

查看试题解析
11. 已知函数 $f (x) = {\begin{matrix} {(\frac{1}{2})}^{x} ， x \leq \frac{1}{2} \\ l o g_{\frac{1}{2}} x ， x > \frac{1}{2} . \end{matrix}$ 若f（x）的图象与直线y=kx有两个不同的交点，则实数k的取值范围为．

查看试题解析
12. 已知函数f（x）同时满足以下条件：
①定义域为R；
②值域为[0，1]；
③f（x）﹣f（﹣x）=0．
试写出一个函数解析式f（x）= ．

查看试题解析
13. 某罐头生产厂计划制造一种圆柱形的密封铁皮罐头盒，其表面积为定值S．若罐头盒的底面半径为r，则罐头盒的体积V与r的函数关系式为；当r=时，罐头盒的体积最大．

查看试题解析
14. 将集合M={1，2，3，…15}表示为它的5个三元子集（三元集：含三个元素的集合）的并集，并且这些三元子集的元素之和都相等，则每个三元集的元素之和为；请写出满足上述条件的集合M的5个三元子集．（只写出一组）

查看试题解析

三、解答题

15. 已知数列{a_n}的前n项和为S_n（n∈N^*），满足S_n=2a_n﹣1．
（1）求数列{a_n}的通项公式；
（2）若数列{b_n}满足 $b_{n} = l o g_{\frac{1}{2}} a_{n}$ ，求数列{b_n}的前n项和T_n ．

查看试题解析
16. 已知函数 $f (x) = 2 s i n x \cdot c o s (x - \frac{π}{3})$ ．
（1）求函数f（x）的最小正周期；
（2）当 $x \in [0 ， \frac{π}{2}]$ 时，求函数f（x）的取值范围．

查看试题解析
17. 在△ABC中， $∠A = \frac{π}{4}$ ， $\frac{c}{b} = \frac{3 \sqrt{2}}{7}$ ．
（1）试求tanC的值；
（2）若a=5，试求△ABC的面积．

查看试题解析
18. 已知函数f（x）=（x²﹣ax+a）•e^﹣x ， a∈R．
（1）求函数f（x）的单调区间；
（2）设g（x）=f'（x），其中f'（x）为函数f（x）的导函数．判断g（x）在定义域内是否为单调函数，并说明理由．

查看试题解析
19. 已知函数 $f (x) = \frac{1}{e^{x}} - l n x - \frac{2}{e x}$ ．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）求证： $l n x \geq - \frac{1}{e x}$ ；
（3）判断曲线y=f（x）是否位于x轴下方，并说明理由．

查看试题解析
20. 数列a₁ ， a₂ ， …，a_n是正整数1，2，…，n的任一排列，且同时满足以下两个条件：
①a₁=1；②当n≥2时，|a_i﹣a_i+1|≤2（i=1，2，…，n﹣1）．
记这样的数列个数为f（n）．
（ 1）写出f（2），f（3），f（4）的值；
（ 2）证明f（2018）不能被4整除．

查看试题解析