2015-2016学年山东省济宁市曲阜市八年级下学期期中数学试卷

试卷更新日期：2016-10-13 类型：期中考试

进入出卷网下载

一、选择题

1. 要使式子 $\sqrt{2 + x}$ 有意义，则x的取值范围是（　　）

A、x≤﹣2 B、x≤2 C、x≥2 D、x≥﹣2

查看试题解析
2. 下列二次根式中能与 $\sqrt{2}$ 合并的二次根式的是（　　）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{3}{2}}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{18}$

查看试题解析
3. 平行四边形、矩形、菱形、正方形中是轴对称图形的有（　　）个．

A、1 B、2 C、3 D、4

查看试题解析
4. 下列各组数中，能成为直角三角形的三条边长的是（　　）

A、8、15、17 B、10、24、25 C、9、15、20 D、9、80、81

查看试题解析
5. 直角三角形的两条直角边的长分别为5，12，则斜边上的高线的长为（　　）

A、 $\frac{80}{13}$ cm B、13cm C、 $\frac{13}{2}$ cm D、 $\frac{60}{13}$ cm

查看试题解析
6. 下列条件中，不能判断四边形ABCD是平行四边形的是（　　）

A、∠A=∠C，∠B=∠D B、AB∥CD，AB=CD C、AB=CD，AD∥BC D、AB∥CD，AD∥BC

查看试题解析
7. 如图，在菱形ABCD中，AB=5，∠B：∠BCD=1：2，则对角线AC等于（）

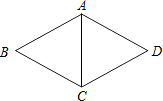A、5 B、10 C、15 D、20

查看试题解析
8.
如图，把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′，则它们的公共部分的面积等于（）

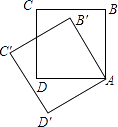A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{3 \sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
9. 将矩形纸片ABCD按如图所示的方式折叠．恰好得到菱形AECF．若AD= $\sqrt{3}$ ，则菱形AECF的面积为（）

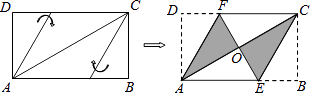A、2 $\sqrt{3}$ B、4 $\sqrt{3}$ C、4 D、8

查看试题解析
10. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（　　）

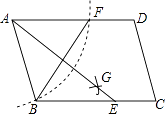A、4 B、6 C、8 D、10

查看试题解析

二、填空题

11. 相邻两边长分别是2+ $\sqrt{3}$ 与2﹣ $\sqrt{3}$ 的平行四边形的周长是

查看试题解析
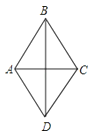
12.
如图，在菱形ABCD中，对角线AC=6，BD=8，则这个菱形的边长为

查看试题解析
13. 已知x= $\sqrt{3}$ +1，y= $\sqrt{3}$ ﹣1，则代数式 $\frac{y}{x}$ + $\frac{x}{y}$ 的值是

查看试题解析
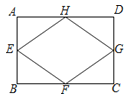
14.
如图，已知矩形ABCD的对角线长为8cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长等于cm．

查看试题解析
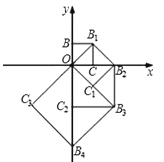
15.
如图，点O（0，0），B（0，1）是正方形OBB₁C的两个顶点，以它的对角线OB₁为一边作正方形OB₁B₂C₁ ，以正方形OB₁B₂C₁的对角线OB₂为一边作正方形OB₂B₃C₂ ，再以正方形OB₂B₃C₂的对角线OB₃为一边作正方形OB₃B₄C₃ ， …，依次进行下去，则点B₆的坐标是

查看试题解析

三、解答题

16. 计算下列各式

(1)、 $\sqrt{14} \div \sqrt{6}$ × $\sqrt{\frac{27}{2}}$ ；

(2)、（ $\sqrt{0.5}$ ﹣2 $\sqrt{\frac{1}{3}}$ ）﹣（ $\sqrt{\frac{1}{8}}$ ﹣ $\sqrt{75}$ ）；

(3)、（7+4 $\sqrt{3}$ ）（7﹣4 $\sqrt{3}$ ）﹣（ $\sqrt{3}$ ﹣1）² ．

查看试题解析
17. 如图，一架长2.5m的梯子，斜靠在一竖直的墙上，这时，梯底距墙底端0.7m，如果梯子的顶端沿墙下滑0.4m，则梯子的底端将滑出多少米？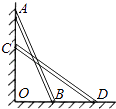

查看试题解析
18. 如图，在矩形ABCD中．点O在边AB上，∠AOC=∠BOD．求证：AO=OB．

查看试题解析
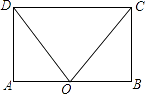19. 如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．

查看试题解析
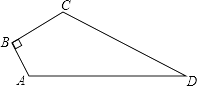20. 如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角．
实验与操作：
根据要求进行尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）

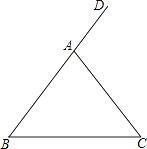(1)、作∠DAC的平分线AM；

(2)、作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE，CF．
猜想并证明：
判断四边形AECF的形状并加以证明．

查看试题解析
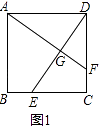
21. 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．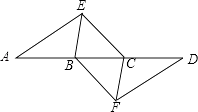

(1)、求证：四边形BFCE是平行四边形；

(2)、若AD=10，DC=3，∠EBD=60°，则BE=时，四边形BFCE是菱形．

查看试题解析
22. 已知E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．
试探究下列问题：

(1)、
如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）

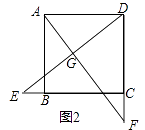
(2)、
如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；

(3)、
如图3，在（2）的基础上，连接AE和EF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．

查看试题解析